
【题目】连续投骰子两次得到的点数分别为m,n,作向量![]() (m,n),则
(m,n),则![]() 与
与![]() (1,﹣1)的夹角成为直角三角形内角的概率是_____.
(1,﹣1)的夹角成为直角三角形内角的概率是_____.
科目:高中数学 来源: 题型:
【题目】如图,四边形![]() 是边长为2的菱形,且
是边长为2的菱形,且![]() .四边形
.四边形![]() 是平行四边形,且
是平行四边形,且![]() .点
.点![]() ,
,![]() 在平面
在平面![]() 内的射影为
内的射影为![]() ,
,![]() ,且
,且![]() 在
在![]() 上,四棱锥
上,四棱锥![]() 的体积为2.
的体积为2.
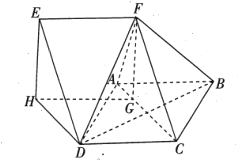
(1)求证:平面![]() 平面
平面![]() ;
;
(2)在![]() 上是否存在点
上是否存在点![]() ,使
,使![]() 平面
平面![]() ?如果存在,是确定点
?如果存在,是确定点![]() 的位置,如果不存在,请说明理由.
的位置,如果不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】据历史记载,美日在中途岛(Midway)海战前,美方截获了日方密码电报,据美方已破译的密码得知,日方将向某岛进行军事活动,但关键含有地点的部分却被日方换成了另一种密码.经专家研究,估计是一种密匙密码,且密匙为3位.所谓密匙密码是指:将一段英文字母的明文(未加密前原文)经过对某一组数字(即密匙)的变换,改变成了另一组英文字母成为密文(加密后的文字)例如:明文:![]() (不计空格,不计大小写)在密匙为:1 9 2的条件下,变换过程如下图所示:
(不计空格,不计大小写)在密匙为:1 9 2的条件下,变换过程如下图所示:
s | t | u | d | e | n | t |
1 | 9 | 2 | 1 | 9 | 2 | 1 |
t | c | w | e | n | p | u |
则密文为:![]() ,试根据上面信息回答下面问题:
,试根据上面信息回答下面问题:
(1)在密匙为111的条件下,填写下表,并写出密文;
s | t | u | d | e | n | t |
密文____________________.
(2)若![]()
![]() 请填写下表,并写出密匙;
请填写下表,并写出密匙;
s | t | u | d | e | n | t |
密匙为_____________.
(3)若下面即是那段包含地点(Midway)的破译不出的密文:![]() ,且此段密文也是3位密匙加密,试填写下表,写出密匙,并将此段密文翻译成明文.(不必证明,写出明文即可)
,且此段密文也是3位密匙加密,试填写下表,写出密匙,并将此段密文翻译成明文.(不必证明,写出明文即可)
c | w | b | c | f | s | o | l | l | y | d | g |
密匙为___________,明文为_________.
查看答案和解析>>
科目:高中数学 来源: 题型:
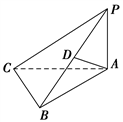
【题目】如图所示,在三棱锥P–ABC中,PA⊥平面ABC,D是棱PB的中点,已知PA=BC=2,AB=4,CB⊥AB,则异面直线PC,AD所成角的余弦值为
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某城市为了解游客人数的变化规律,提高旅游服务质量,收集并整理了2017年1月至2019年12月期间月接待游客量(单位:万人)的数据,绘制了下面的折线图.根据该折线图,下列结论错误的是( )

A.年接待游客量逐年增加
B.各年的月接待游客量高峰期大致在8月
C.2017年1月至12月月接待游客量的中位数为30万人
D.各年1月至6月的月接待游客量相对于7月至12月,波动性更小,变化比较平稳
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图①在直角梯形ABCP中,![]() ,
,![]() ,
,![]() ,
,![]() ,E,F,G分别是线段PC,PD,BC的中点,现将
,E,F,G分别是线段PC,PD,BC的中点,现将![]() 折起,使平面
折起,使平面![]() 平面ABCD如图②.
平面ABCD如图②.
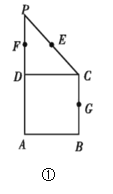
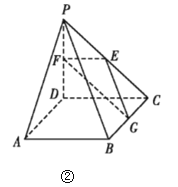
(1)求证:![]() 平面EFG;
平面EFG;
(2)求二面角G—EF—D的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,某地出土的一种“钉”是由四条线段组成,其结构能使它任意抛至水平面后,总有一端所在的直线竖直向上,并记组成该“钉”的四条线段的公共点为O,钉尖为![]() .
.
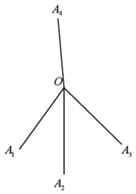
⑴设![]() ,当
,当![]() ,
,![]() ,
,![]() 在同一水平面内时,求
在同一水平面内时,求![]() 与平面
与平面![]() 所成角的大小
所成角的大小![]() 结果用反三角函数值表示
结果用反三角函数值表示![]() .
.
⑵若该“钉”的三个钉尖所确定的三角形的面积为![]() ,要用某种线型材料复制100枚这种“钉”
,要用某种线型材料复制100枚这种“钉”![]() 损耗忽略不计
损耗忽略不计![]() ,共需要该种材料多少米?
,共需要该种材料多少米?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2019年国际篮联篮球世界杯,将于2019年在的北京、广州、南京、上海、武汉、深圳、佛山、东莞八座城市举行.为了宣传世界杯,某大学从全校学生中随机抽取了![]() 名学生,对是否收看篮球世界杯赛事的情况进行了问卷调查,统计数据如下:
名学生,对是否收看篮球世界杯赛事的情况进行了问卷调查,统计数据如下:
会收看 | 不会收看 | |
男生 | 60 | 20 |
女生 | 20 | 20 |
(1)根据上表说明,能否有![]() 的把握认为收看篮球世界杯赛事与性别有关?
的把握认为收看篮球世界杯赛事与性别有关?
(2)现从参与问卷调查且收看篮球世界杯赛事的学生中,采用按性别分层抽样的方法选取![]() 人参加2019年国际篮联篮球世界杯赛志愿者宣传活动.
人参加2019年国际篮联篮球世界杯赛志愿者宣传活动.
(i)求男、女学生各选取多少人;
(ii)若从这![]() 人中随机选取
人中随机选取![]() 人到校广播站开展2019年国际篮联篮球世界杯赛宣传介绍,求恰好选到
人到校广播站开展2019年国际篮联篮球世界杯赛宣传介绍,求恰好选到![]() 名男生的概率.
名男生的概率.
附: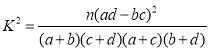 ,其中
,其中![]() .
.
|
|
|
|
|
|
|
|
|
|
|
|
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com