
【题目】如图,![]() 为圆
为圆![]() 的直径,点
的直径,点![]() 为圆
为圆![]() 上的一点,且
上的一点,且![]() ,点
,点![]() 为线段
为线段![]() 上一点,且
上一点,且![]() ,
,![]() 垂直圆
垂直圆![]() 所在的平面.
所在的平面.
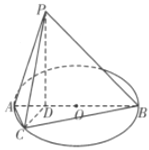
(Ⅰ)求证:![]() 平面
平面![]() ;
;
(Ⅱ)若![]() ,求二面角
,求二面角![]() 的余弦值.
的余弦值.
 浙江名校名师金卷系列答案
浙江名校名师金卷系列答案科目:高中数学 来源: 题型:
【题目】某校举行数学、物理、化学、生物四科竞赛,甲、乙、丙、丁分别参加其中的一科竞赛,且没有两人参加同一科竞赛.①甲没有参加数学生物竞赛;②乙没有参加化学、生物竞赛;③若甲参加化学竞赛,则丙不参加生物竞赛;④丁没有参加数学、化学竞赛;⑤丙没有参加数学、化学竞赛.若以上命题都是真命题,那么丁参加的竞赛科目是__________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】《论语·子路》篇中说:“名不正,则言不顺;言不顺,则事不成;事不成,则礼乐不兴;礼乐不兴,则刑罚不中;刑罚不中,则民无所措手足”,所以,名不正,则民无所措手足.上述推理过程用的是( )
A. 类比推理 B. 归纳推理 C. 演绎推理 D. 合情推理
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】由①安梦怡是高二(1)班的学生,②安梦怡是独生子女,③高二(1)班的学生都是独生子女,写一个“三段论”形式的推理,则大前提,小前提和结论分别为( )
A. ②①③ B. ③①② C. ①②③ D. ②③①
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某班有42名男生,30名女生,已知男女身高各有明显不同,现欲调查平均身高,若采用分层抽样方法,抽取男生1人,女生1人,这种做法是否合适,若不合适,应怎样抽取?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设集合A={x|x>-1},B={x||x|≥1},则“x∈A且xB”成立的充要条件是( )
A. -1<x≤1 B. x≤1
C. x>-1 D. -1<x<1
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某设备在正常运行时,产品的质量![]() ,其中
,其中![]()
![]() ,
,![]() .为了检验设备是否正常运行,质量检查员需要随机的抽取产品,测其质量.
.为了检验设备是否正常运行,质量检查员需要随机的抽取产品,测其质量.
(1)当质量检查员随机抽检时,测得一件产品的质量为![]()
![]() ,他立即要求停止生产,检查设备.请你根据所学知识,判断该质量检查员的决定是否有道理,并说明你判断的依据;
,他立即要求停止生产,检查设备.请你根据所学知识,判断该质量检查员的决定是否有道理,并说明你判断的依据;
进而,请你揭密质量检测员做出“要求停止生产,检查设备”的决定时他参照的质量参数标准;
(2)请你根据以下数据,判断优质品与其生产季节有关吗?

(3)该质量检查员从其住宅小区到公司上班的途中要经过![]() 个有红绿灯的十字路口,假设他在每个十字路口遇到红灯或绿灯是相互独立的,并且概率均为
个有红绿灯的十字路口,假设他在每个十字路口遇到红灯或绿灯是相互独立的,并且概率均为![]() .求该质量检查员在上班途中遇到红灯的期望和方差.
.求该质量检查员在上班途中遇到红灯的期望和方差.
参考数据:


查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列叙述错误的是( )
A. 若事件A发生的概率为P(A),则0≤P(A)≤1
B. 互斥事件不一定是对立事件,但是对立事件一定是互斥事件
C. 两个对立事件的概率之和为1
D. 对于任意两个事件A和B,都有P(A∪B)=P(A)+P(B)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com