
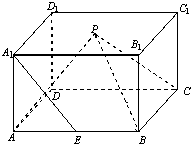
 如图,P是正四棱柱ABCD-A1B1C1D1上底面的中心,E是AB的中点,AB=
如图,P是正四棱柱ABCD-A1B1C1D1上底面的中心,E是AB的中点,AB=| 2 |
| 2 |

| 2 |
| 2 |
| ||
| 2 |
| 2 |
| 2 |
| 2 |
| 2 |
| ||
| 2 |
| ||
| 2 |
| BC |
| 2 |
| PB |
| ||
| 2 |
| ||
| 2 |
| A1E |
| ||
| 2 |
| PA |
| ||
| 2 |
| ||
| 2 |
| v |
|
|
| v |
| 2 |
| A1E |
| v |
| A1E |
| v |
| v |
| 2 |
| v |
| PA |
| ||||
|
|
| -2 | ||
|
| ||
| 3 |
| v |
| PA |
| ||
| 3 |
| ||
| 3 |


科目:高中数学 来源: 题型:
(08年江西卷理)如图1,一个正四棱柱形的密闭容器底部镶嵌了同底的正四棱锥形实心装饰块,容器内盛有![]() 升水时,水面恰好经过正四棱锥的顶点P。如果将容器倒置,水面也恰好过点
升水时,水面恰好经过正四棱锥的顶点P。如果将容器倒置,水面也恰好过点![]() (图2)。有下列四个命题:
(图2)。有下列四个命题:
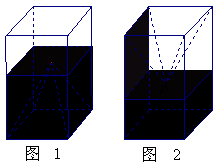
A.正四棱锥的高等于正四棱柱高的一半
B.将容器侧面水平放置时,水面也恰好过点![]()
C.任意摆放该容器,当水面静止时,水面都恰好经过点![]()
D.若往容器内再注入![]() 升水,则容器恰好能装满
升水,则容器恰好能装满
其中真命题的代号是: (写出所有真命题的代号).
查看答案和解析>>
科目:高中数学 来源:2014届重庆市高二上学期10月月考考理科数学试卷(解析版) 题型:填空题
如图1,一个正四棱柱形的密闭容器水平放置,其底部镶嵌了同底的正四棱锥形实心装饰块,容器内盛有a升水时,水面恰好经过正四棱锥的顶点P.如果将容器倒置,水面也恰好过点P(图2).有下列四个命题:
A.正四棱锥的高等于正四棱柱高的一半
B.将容器侧面水平放置时,水面也恰好过点P
C.任意摆放该容器,当水面静止时,水面都恰好经过点P
D.若往容器内再注入a升水,则容器恰好能装满
其中真命题的代号是 .(写出所有真命题的代号) .
查看答案和解析>>
科目:高中数学 来源:2013届上海市高二年级期终考试数学 题型:填空题
如图1,一个正四棱柱形的密闭容器底部镶嵌了同底的正四棱锥形实心装饰块,容器内盛有 升水时,水面恰好经过正四棱锥的顶点P.如果将容器倒置,水面也恰好过点
升水时,水面恰好经过正四棱锥的顶点P.如果将容器倒置,水面也恰好过点 (图2).有下列四个命题:
(图2).有下列四个命题:
A.正四棱锥的高等于正四棱柱高的一半;
B.将容器侧面水平放置时,水面也恰好过点 ;
;
C.任意摆放该容器,当水面静止时,水面都恰好经过点 ;
;
D.若往容器内再注入 升水,则容器恰好能装满.
升水,则容器恰好能装满.
其中真命题的代号是:___________________(写出所有真命题的代号).

查看答案和解析>>
科目:高中数学 来源:河北省2009-2010学年度第二学期二调考试高一年级数学试卷理科 题型:填空题
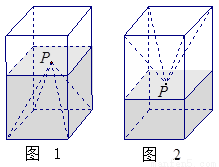
如图1,一个正四棱柱形的密闭容器底部镶嵌了同底的正四棱锥形实心装饰块,容器内盛有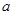 升水时,水面恰好经过正四棱锥的顶点P。如果将容器倒置,水面也恰好过点
升水时,水面恰好经过正四棱锥的顶点P。如果将容器倒置,水面也恰好过点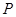 (图2)。有下列四个命题:
(图2)。有下列四个命题:
A.正四棱锥的高等于正四棱柱高的一半
B.将容器侧面水平放置时,水面也恰好过点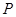
C.若往容器内再注入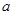 升水,则容器恰好能装满;
升水,则容器恰好能装满;
其中正确的序号是:
查看答案和解析>>
科目:高中数学 来源:2008年普通高等学校招生全国统一考试理科数学(江西卷) 题型:选择题
如图1,一个正四棱柱形的密闭容器底部镶嵌了同底的正四棱锥形实心装饰块,容器内盛有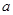 升水时,水面恰好经过正四棱锥的顶点P。如果将容器倒置,水面也恰好过点
升水时,水面恰好经过正四棱锥的顶点P。如果将容器倒置,水面也恰好过点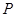 (图2)。有下列四个命题:
(图2)。有下列四个命题:
A.正四棱锥的高等于正四棱柱高的一半
B.将容器侧面水平放置时,水面也恰好过点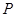
C.任意摆放该容器,当水面静止时,水面都恰好经过点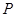
D.若往容器内再注入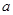 升水,则容器恰好能装满
升水,则容器恰好能装满
其中真命题的代号是: (写出所有真命题的代号)。

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com