
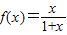 .设数列{an}满足a1=1,an+1=f(an)(n∈N+).
.设数列{an}满足a1=1,an+1=f(an)(n∈N+).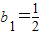 ,
,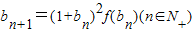 ,求证:对一切正整数n≥1都有
,求证:对一切正整数n≥1都有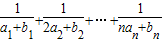 <2.
<2.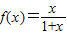 ,an+1=f(an)(n∈N+)知:
,an+1=f(an)(n∈N+)知: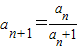 ,由此能求出
,由此能求出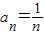 .
.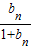 ,知bn+1=bn(bn+1),故
,知bn+1=bn(bn+1),故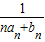 =
=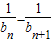 ,由此利用裂项求法能够证明对一切正整数n≥1都有
,由此利用裂项求法能够证明对一切正整数n≥1都有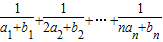 <2.
<2.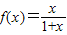 ,an+1=f(an)(n∈N+),
,an+1=f(an)(n∈N+),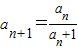 ,…1分
,…1分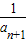 =
=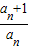 ,…..3分
,…..3分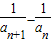 =1,…5分
=1,…5分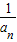 }是以
}是以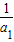 为首项,1为公差的等差数列,
为首项,1为公差的等差数列, ,
,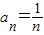 .…6分
.…6分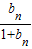 ,
,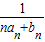 =
=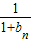 =
=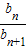 =
= =
=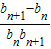 =
=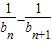 ,…9分
,…9分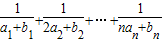
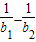 )+(
)+(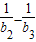 )+…+(
)+…+(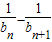 )
)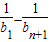
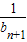 <2.…11分
<2.…11分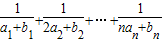 <2.…12分
<2.…12分

科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
| x+1-a | a-x |
查看答案和解析>>
科目:高中数学 来源: 题型:
| ||
| 1-x |
| 1 |
| n |
| 2 |
| n |
| n-1 |
| n |
| 1 |
| a1 |
| 1 |
| a2 |
| 1 |
| an |
| sinα | ||
|
查看答案和解析>>
科目:高中数学 来源:学习周报 数学 人教课标高二版(A必修5) 2009-2010学年 第5期 总第161期 人教课标版(A必修5) 题型:044
已知函数f(x)=![]() (a,b为常数,a≠0),满足f(2)=1,且f(x)=x有两个相同的根.
(a,b为常数,a≠0),满足f(2)=1,且f(x)=x有两个相同的根.
(1)求f(x)的表达式;
(2)设数列{xn}满足xn+1=f(xn),且x1>0,证明数列{![]() }是等差数列.
}是等差数列.
查看答案和解析>>
科目:高中数学 来源:2008年普通高等学校招生全国统一考试(福建卷)、数学(理) 题型:044
已知函数![]() .
.
(Ⅰ)设{an}是正数组成的数列,前n项和为Sn,其中a1=3.若点![]() (n∈N*)在函数y=
(n∈N*)在函数y=![]() 的图象上,求证:点(n,Sn)也在y=
的图象上,求证:点(n,Sn)也在y=![]() 的图象上;
的图象上;
(Ⅱ)求函数f(x)在区间(a-1,a)内的极值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com