
【题目】2018年11月21日,意大利奢侈品牌“![]() ﹠
﹠![]() ”在广告中涉嫌辱华,中国明星纷纷站出来抵制该品牌,随后京东、天猫、唯品会等中国电商平台全线下架了该品牌商品,当天有大量网友关注此事件,某网上论坛从关注此事件跟帖中,随机抽取了100名网友进行调查统计,先分别统计他们在跟帖中的留言条数,再把网友人数按留言条数分成6组:
”在广告中涉嫌辱华,中国明星纷纷站出来抵制该品牌,随后京东、天猫、唯品会等中国电商平台全线下架了该品牌商品,当天有大量网友关注此事件,某网上论坛从关注此事件跟帖中,随机抽取了100名网友进行调查统计,先分别统计他们在跟帖中的留言条数,再把网友人数按留言条数分成6组:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,得到如图所示的频率分布直方图;
,得到如图所示的频率分布直方图;

并将其中留言不低于40条的规定为“强烈关注”,否则为“一般关注”,对这100名网友进一步统计得到列联表的部分数据如下表.
一般关注 | 强烈关注 | 合计 | |
男 | 45 | ||
女 | 10 | 55 | |
合计 | 100 |
(1)在答题卡上补全列联表中数据;并判断能否有95%的把握认为网友对此事件是否为“强烈关注”与性别有关?
(2)现已从“强烈关注”的网友中按性别分层抽样选取了5人,再从这5人中选取2人,求这2人中至少有1名女性的概率.
参考公式及数据:![]() ,
,
| 0.05 | 0.010 |
| 3.841 | 6.635 |
【答案】(1)没有![]() 的把握认为网友对此事件是否为“强烈关注”与性别有关;(2)
的把握认为网友对此事件是否为“强烈关注”与性别有关;(2)![]() .
.
【解析】
(1)根据题意得到列联表,然后根据题中数据求出![]() 的值,最后根据临界值表中的数据得到结论.(2)由题意得到所选的5人中的男性、女性的个数,然后通过列举法得到所有的基本事件个数及至少有一名女性包含的事件的个数,最后根据古典概型概率公式求解即可.
的值,最后根据临界值表中的数据得到结论.(2)由题意得到所选的5人中的男性、女性的个数,然后通过列举法得到所有的基本事件个数及至少有一名女性包含的事件的个数,最后根据古典概型概率公式求解即可.
(1)由题意得列联表如下:
一般关注 | 强烈关注 | 合计 | |
男 | 30 | 15 | 45 |
女 | 45 | 10 | 55 |
合计 | 75 | 25 | 100 |
由表中数据可得
![]() ,
,
所以没有95%的把握认为网友对此事件是否为“强烈关注”与性别有关.
(2)从“强烈关注”的网友所选的5人中,男性人数为![]() 人,分别记为
人,分别记为![]() ,女性人数为
,女性人数为![]() 人,分别记为
人,分别记为![]() .
.
从这5人中任选2人的所有结果为:![]() ,共10种,且它们是等可能的,
,共10种,且它们是等可能的,
其中至少有一名女性网友的结果为:![]() ,共7种,
,共7种,
所以所求概率为![]() .
.
即这2人中至少有1名女性的概率![]() .
.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】某化工企业2018年年底投入100万元,购入一套污水处理设备。该设备每年的运转费用是0.5万元,此外,每年都要花费一定的维护费,第一年的维护费为2万元,由于设备老化,以后每年的维护费都比上一年增加2万元。设该企业使用该设备![]() 年的年平均污水处理费用为
年的年平均污水处理费用为![]() (单位:万元)
(单位:万元)
(1)用![]() 表示
表示![]() ;
;
(2)当该企业的年平均污水处理费用最低时,企业需重新更换新的污水处理设备。则该企业几年后需要重新更换新的污水处理设备。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】过抛物线![]() 的焦点
的焦点![]() 且斜率为1的直线与抛物线
且斜率为1的直线与抛物线![]() 交于
交于![]() 、
、![]() 两点,且
两点,且![]() .
.
(1)求抛物线![]() 的方程;
的方程;
(2)点![]() 是抛物线
是抛物线![]() 上异于
上异于![]() 、
、![]() 的任意一点,直线
的任意一点,直线![]() 、
、![]() 与抛物线
与抛物线![]() 的准线分别交于点
的准线分别交于点![]() 、
、![]() ,求证:
,求证:![]() 为定值.
为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
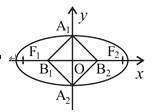
【题目】如图,已知椭圆![]()
![]() 的左、右焦点分别为
的左、右焦点分别为![]() ,
,![]() ,短轴的两端点分别为
,短轴的两端点分别为![]() ,
,![]() ,线段
,线段![]() ,
,![]() 的中点分别为
的中点分别为![]() ,
,![]() ,且四边形
,且四边形![]() 是面积为8的矩形.
是面积为8的矩形.
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)过![]() 作直线
作直线![]() 交椭圆于
交椭圆于![]() ,
,![]() 两点,若
两点,若![]() ,求直线
,求直线![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】算筹是在珠算发明以前我国独创并且有效的计算工具,为我国古代数学的发展做出了很大贡献.在算筹计数法中,以“纵式”和“横式”两种方式来表示数字,如图:

表示多位数时,个位用纵式,十位用横式,百位用纵式,千位用横式,以此类推,遇零则置空,如图:
![]()
如果把5根算筹以适当的方式全部放入 下面的表格中,那么可以表示的三位数的个数为( )
![]()
A. ![]()
B. ![]()
C. ![]()
D. ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com