
【题目】如图所示为一名曰“堑堵”的几何体,已知 AE⊥底面BCFE , DF ∥ AE , DF = AE = 1, CE =![]() ,四边形ABCD 是正方形.
,四边形ABCD 是正方形.
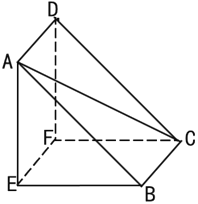
(1)《九章算术》中将四个面都是直角三角形的四面体称为鳖臑.判断四面体 EABC 是否为鳖臑,若是,写出其 每一个面的直角,并证明;若不是,请说明理由.
(2)求四面体 EABC 的体积.
 综合自测系列答案
综合自测系列答案科目:高中数学 来源: 题型:
【题目】如图,△![]() 为一个等腰三角形形状的空地,腰
为一个等腰三角形形状的空地,腰![]() 的长为
的长为![]() (百米),底
(百米),底![]() 的长为
的长为![]() (百米),现决定在空地内筑一条笔直的小路
(百米),现决定在空地内筑一条笔直的小路![]() (宽度不计),将该空地分成一个四边形和一个三角形,设分成的四边形和三角形的周长相等.
(宽度不计),将该空地分成一个四边形和一个三角形,设分成的四边形和三角形的周长相等.

(1)若小路一端![]() 为
为![]() 的中点,求此时小路的长度;
的中点,求此时小路的长度;
(2)求分成的四边形的面积的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知有穷数列![]() 共有
共有![]() 项
项![]() ,首项
,首项![]() ,设该数列的前
,设该数列的前![]() 项和为
项和为![]() ,且
,且![]()
![]() 其中常数
其中常数![]() .
.
(1)求证:数列![]() 是等比数列
是等比数列
(2)若![]() ,数列
,数列![]() 满足
满足![]()
![]() ,求出数列
,求出数列![]() 的通项公式
的通项公式
(3)若(2)中的数列![]() 满足不等式
满足不等式![]() ,求出
,求出![]() 的值
的值
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
(1)求函数![]() 的最小正周期;
的最小正周期;
(2)将函数![]() 的图象向右平移
的图象向右平移![]() 个单位长度,再向下平移
个单位长度,再向下平移![]() (
(![]() )个单位长度后得到函数
)个单位长度后得到函数![]() 的图象,且函数
的图象,且函数![]() 的最大值为2.
的最大值为2.
(ⅰ)求函数![]() 的解析式; (ⅱ)证明:存在无穷多个互不相同的正整数
的解析式; (ⅱ)证明:存在无穷多个互不相同的正整数![]() ,使得
,使得![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com