
已知向量 函数
函数 的第
的第 个零点记作
个零点记作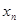 (从小到大依次计数),所有
(从小到大依次计数),所有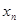 组成数列
组成数列 .
.
(1)求函数 的值域;
的值域;
(2)若 ,求数列
,求数列 的前100项和
的前100项和 .
.
科目:高中数学 来源: 题型:解答题
已知 为坐标原点,
为坐标原点, =(
=( ),
), =(1,
=(1, ),
),  .
.
(1)若 的定义域为[-
的定义域为[- ,
, ],求y=
],求y= 的单调递增区间;
的单调递增区间;
(2)若 的定义域为[
的定义域为[ ,
, ],值域为[2,5],求
],值域为[2,5],求 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知向量a= ,b=(
,b=(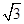 sinx,cos2x),x∈R,设函数f(x)=a·b.
sinx,cos2x),x∈R,设函数f(x)=a·b.
(1)求f(x)的最小正周期.
(2)求f(x)在 上的最大值和最小值.
上的最大值和最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知椭圆C: +
+ =1(a>b>0)的离心率e=
=1(a>b>0)的离心率e= ,椭圆C的上、下顶点分别为A1,A2,左、右顶点分别为B1,B2,左、右焦点分别为F1,F2.原点到直线A2B2的距离为
,椭圆C的上、下顶点分别为A1,A2,左、右顶点分别为B1,B2,左、右焦点分别为F1,F2.原点到直线A2B2的距离为 .
.
(1)求椭圆C的方程;
(2)过原点且斜率为 的直线l,与椭圆交于E,F点,试判断∠EF2F是锐角、直角还是钝角,并写出理由;
的直线l,与椭圆交于E,F点,试判断∠EF2F是锐角、直角还是钝角,并写出理由;
(3)P是椭圆上异于A1,A2的任一点,直线PA1,PA2,分别交 轴于点N,M,若直线OT与过点M,N 的圆G相切,切点为T.证明:线段OT的长为定值,并求出该定值.
轴于点N,M,若直线OT与过点M,N 的圆G相切,切点为T.证明:线段OT的长为定值,并求出该定值.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知 =(cosα,sinα),
=(cosα,sinα), =(cosβ,sinβ),
=(cosβ,sinβ), 与
与 之间有关系|k
之间有关系|k +
+ |=
|= |
| -k
-k |,其中k>0,(Ⅰ)用k表示
|,其中k>0,(Ⅰ)用k表示 ;
;
(Ⅱ)求 ·
· 的最小值,并求此时
的最小值,并求此时 与
与 的夹角的大小。
的夹角的大小。
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本题满分14分)已知两个不共线的向量 ,它们的夹角为
,它们的夹角为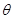 ,且
,且 ,
, ,
, 为正实数.
为正实数.
(1)若 与
与 垂直,求
垂直,求 ;
;
(2)若 ,求
,求 的最小值及对应的
的最小值及对应的 的值,并判断此时向量
的值,并判断此时向量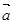 与
与 是否垂直?
是否垂直?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com