练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】已知各项均为正数数列的前项和满足.

    （1）求数列的通项公式;；

    （2）若数列满足，求数列的前项和.

    【答案】（1）；（2）.

    【解析】试题分析：（1）由得，∴，于是可得，；（2）根据（1）求得，

    ∴，利用裂项相消法可求得数列的前项和.

    试题解析：（1）∵，

    ∴.

    又数列各项均为正数，

    ∴，∴，∴.

    当时，；

    当时，，

    又∵也满足上式，∴.

    （2）据（1）求解，得，

    ∴.

    ∴数列的前项和

    .

    【方法点晴】本题主要考查等差数列的通项以及裂项相消法求数列的和，属于中档题. 裂项相消法是最难把握的求和方法之一，其原因是有时很难找到裂项的方向，突破这一难点的方法是根据式子的结构特点，常见的裂项技巧：(1)；（2） ； （3）；（4） ；此外，需注意裂项之后相消的过程中容易出现丢项或多项的问题，导致计算结果错误.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】从8名运动员中选4人参加米接力赛，在下列条件下，各有多少种不同的排法？

    （1）甲、乙两人必须入选且跑中间两棒；

    （2）若甲、乙两人只有一人被选且不能跑中间两棒；

    （3）若甲、乙两人都被选且必须跑相邻两棒；

    （4）甲不在第一棒.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知p：方程x2＋(m2－6m)y2＝1表示双曲线，q：函数f(x)＝x3－mx2＋(2m＋3)x在(－∞，＋∞)上是单调增函数．

    （1）若p是真命题，求实数m的取值范围；

    （2）若p或q是真命题，p且q是假命题，求实数m的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】△ABC的内角A，B，C所对应的边分别为a，b，c．

    （Ⅰ）若a，b，c成等差数列，证明：sinA+sinC=2sin（A+C）；

    （Ⅱ）若a，b，c成等比数列，求cosB的最小值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数，其中为常数且.

    （1）当时，求曲线在点处的切线方程；

    （2）讨论函数的单调性；

    （3）当时，，若存在，使成立，求实数的取值范围.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】下列命题中的说法正确的是（ ）

    A. 若向量，则存在唯一的实数使得；

    B. 命题“若，则”的否命题为“若，则”；

    C. 命题“，使得”的否定是：“，均有”；

    D. 命题“在中，是的充要条件”的逆否命题为真命题.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某市为了考核甲，乙两部门的工作情况，随机访问了50位市民，根据这50位市民对这两部门的评分（评分越高表明市民的评价越高），绘制茎叶图如下：

    （1）分别估计该市的市民对甲，乙两部门评分的中位数；

    （2）分别估计该市的市民对甲，乙两部门的评分高于90的概率；

    （3）根据茎叶图分析该市的市民对甲，乙两部门的评价．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

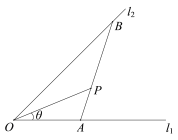
    【题目】如图，某地村庄P与村庄O的距离为千米，从村庄O出发有两条道路，经测量，的夹角为，OP与的夹角满足（其中），现要经过P修一条直路分别与道路交汇于两点，并在处设立公共设施．

    （1）已知修建道路的单位造价分别为2m元/千米和m元/千米，若两段道路的总造价相等，求此时点之间的距离；

    （2）考虑环境因素，需要对段道路进行翻修，段的翻修单价分别为n元/千米和元/千米，要使两段道路的翻修总价最少，试确定点的位置．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数 (， 为自然对数的底数).

    （Ⅰ）求函数的极值；

    （Ⅱ）当时，若直线与曲线没有公共点，求的最大值.

    查看答案和解析>>

    同步练习册答案