
【题目】将圆的一组![]() 等分点分别涂上红色或蓝色,从任意一点开始,按逆时针方向依次记录
等分点分别涂上红色或蓝色,从任意一点开始,按逆时针方向依次记录![]() 个点的颜色,称为该圆的一个“
个点的颜色,称为该圆的一个“![]() 阶段序”,当且仅当两个
阶段序”,当且仅当两个![]() 阶色序对应位置上的颜色至少有一个不相同时,称为不同的
阶色序对应位置上的颜色至少有一个不相同时,称为不同的![]() 阶色序.若某圆的任意两个“
阶色序.若某圆的任意两个“![]() 阶段序”均不相同,则称该圆为“
阶段序”均不相同,则称该圆为“![]() 阶魅力圆”.“3阶魅力圆”中最多可有的等分点个数为( )
阶魅力圆”.“3阶魅力圆”中最多可有的等分点个数为( )
A.4 B.6
C. 8 D.10
 名校提分一卷通系列答案
名校提分一卷通系列答案 课程达标测试卷闯关100分系列答案
课程达标测试卷闯关100分系列答案 新卷王期末冲刺100分系列答案
新卷王期末冲刺100分系列答案 全能闯关100分系列答案
全能闯关100分系列答案科目:高中数学 来源: 题型:
【题目】已知椭圆E的右焦点与抛物线![]() 的焦点重合,点M
的焦点重合,点M![]() 在椭圆E上.
在椭圆E上.
(Ⅰ)求椭圆E的标准方程;
(Ⅱ)设![]() ,直线
,直线![]() 与椭圆E交于A,B两点,若直线PA,PB关于x轴对称,求
与椭圆E交于A,B两点,若直线PA,PB关于x轴对称,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】国庆期间,某旅行社组团去风景区旅游,若旅行团人数在 ![]() 人或
人或 ![]() 人以下,每人需交费用为
人以下,每人需交费用为 ![]() 元;若旅行团人数多于
元;若旅行团人数多于 ![]() 人,则给予优惠:每多
人,则给予优惠:每多 ![]() 人,人均费用减少
人,人均费用减少 ![]() 元,直到达到规定人数
元,直到达到规定人数 ![]() 人为止.旅行社需支付各种费用共计
人为止.旅行社需支付各种费用共计 ![]() 元.
元.
Ⅰ 写出每人需交费用 ![]() 关于人数
关于人数 ![]() 的函数;
的函数;
Ⅱ 旅行团人数为多少时,旅行社可获得最大利润?
查看答案和解析>>
科目:高中数学 来源: 题型:
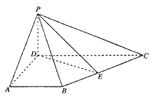
【题目】如图,四边形![]() 为梯形,
为梯形, ![]() ,
, ![]() 平面
平面![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 为
为![]() 中点.
中点.
(1)求证:平面![]() 平面
平面![]() ;
;
(2)线段![]() 上是否存在一点
上是否存在一点![]() ,使
,使![]() 平面
平面![]() ?若有,请找出具体位置,并进行证明:若无,请分析说明理由.
?若有,请找出具体位置,并进行证明:若无,请分析说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设![]() :实数
:实数![]() 满足不等式
满足不等式![]() ,
, ![]() :函数
:函数![]() 无极值点.
无极值点.
(1)若“![]() ”为假命题,“
”为假命题,“![]() ”为真命题,求实数
”为真命题,求实数![]() 的取值范围;
的取值范围;
(2)已知“![]() ”为真命题,并记为
”为真命题,并记为![]() ,且
,且![]() :
: ![]() ,若
,若![]() 是
是![]() 的必要不充分条件,求正整数
的必要不充分条件,求正整数![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】心理学家分析发现“喜欢空间想象”与“性别”有关,某数学兴趣小组为了验证此结论,从全体组员中按分层抽样的方法抽取50名同学(男生30人、女生20人),给每位同学立体几何题、代数题各一道,让各位同学自由选择一道题进行解答,选题情况统计如下表:(单位:人)
立体几何题 | 代数题 | 总计 | |
男同学 | 22 | 8 | 30 |
女同学 | 8 | 12 | 20 |
总计 | 30 | 20 | 50 |
(1)能否有97.5%以上的把握认为“喜欢空间想象”与“性别”有关?
(2)经统计得,选择做立体几何题的学生正答率为![]() ,且答对的学生中男生人数是女生人数的5倍,现从选择做几何题的8名女生中任意抽取两人对她们的答题情况进行研究,记抽取的两人中答对的人数为
,且答对的学生中男生人数是女生人数的5倍,现从选择做几何题的8名女生中任意抽取两人对她们的答题情况进行研究,记抽取的两人中答对的人数为![]() ,求
,求![]() 的分布列及数学期望.
的分布列及数学期望.
附表及公式:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知一次函数f(x)为增函数,且f(f(x))=4x+9,g(x)=mx+m+3(m∈R).
(1)当x∈[-1,2]时,若不等式g(x)>0恒成立,求m的取值范围;
(2)如果函数F(x)=f(x)g(x)为偶函数,求m的值;
(3)当函数f(x)和g(x)满足f(g(x))=g(f(x))时,求函数![]() 的值域.
的值域.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com