
分析 (1)通过设直线l方程:x=ty+m,并与抛物线方程联立,利用A'、O、B三点共线,计算即得结论;
(2)依题意可知A′(-1,y1)、B′(-1,y2),利用S四边形ABB′A′=$\frac{1}{2}$(AA′+BB′)h化简计算即得结论.
解答 解:(1)设$A(\frac{{{y_1}^2}}{4},{y_1}),B(\frac{{{y_2}^2}}{4},{y_2})$,
设直线l方程:x=ty+m,并与抛物线方程联立,
消去x整理得:y2-4ty-4m=0,
∴$\left\{\begin{array}{l}{y_1}+{y_2}=4t\\{y_1}{y_2}=-4m\end{array}\right.$,
依题意A',O,B三点共线,
∴kAO=kBO,即$\frac{{y}_{1}}{-1}$=$\frac{{y}_{2}}{\frac{{{y}_{2}}^{2}}{4}}$,
∴y1y2=-4,
∴m=1;
(2)依题意A′(-1,y1),B′(-1,y2),
S四边形ABB′A′=$\frac{1}{2}$(AA′+BB′)h
=$\frac{1}{2}$($\frac{{{y}_{1}}^{2}}{4}$+1+$\frac{{{y}_{2}}^{2}}{4}$+1)|y1-y2|
=$\frac{1}{2}(\frac{{{y_1}^2+{y_2}^2}}{4}+2)\sqrt{{{({y_1}+{y_2})}^2}-4{y_1}{y_2}}$
=$8({t^2}+1)\sqrt{{t^2}+1}≥8$,
当t=0时等号成立,此时lAB:x=1.
点评 本题考查直线与圆锥曲线的关系,考查运算求解能力,注意解题方法的积累,属于中档题.


 赢在课堂名师课时计划系列答案
赢在课堂名师课时计划系列答案 天天向上课时同步训练系列答案
天天向上课时同步训练系列答案科目:高中数学 来源: 题型:选择题
| A. | 方程$\frac{x}{y-2}=1$表示斜率为1,在y轴上的截距是2的直线 | |
| B. | △ABC的顶点坐标分别为A(0,3),B(-2,0),C(2,0),则中线AO的方程是x=0 | |
| C. | 到x轴距离为5的点的轨迹方程是y=5 | |
| D. | 曲线2x2-3y2-2x+m=0通过原点的充要条件是m=0 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
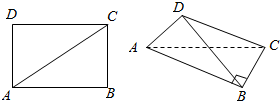 如图,在矩形ABCD中,AB=4,BC=3,沿对角线AC把矩形折成二面角D-AC-B,并且D点在平面ABC内的射影落在AB上.
如图,在矩形ABCD中,AB=4,BC=3,沿对角线AC把矩形折成二面角D-AC-B,并且D点在平面ABC内的射影落在AB上.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [$\frac{π}{4}$,$\frac{π}{3}$]∪[$\frac{2π}{3}$,$\frac{3π}{4}$] | B. | [$\frac{π}{6}$,$\frac{π}{3}$]∪[$\frac{2π}{3}$,$\frac{5π}{6}$] | C. | [$\frac{π}{6}$,$\frac{π}{4}$]∪[$\frac{4π}{3}$,$\frac{5π}{6}$] | D. | [$\frac{π}{4}$,$\frac{π}{3}$]∪[$\frac{2π}{3}$,$\frac{5π}{5}$] |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,⊙O的半径OC垂直于直径AB,M为OB上一点,CM的延长线交⊙O于N,过N点的切线交AB的延长线于P.
如图,⊙O的半径OC垂直于直径AB,M为OB上一点,CM的延长线交⊙O于N,过N点的切线交AB的延长线于P.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
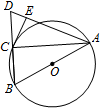 如图,AB是圆O的直径,点C在圆O上,延长BC到D使BC=CD,过C作圆O的切线交AD于E,若AB=8,DC=4,则DE=( )
如图,AB是圆O的直径,点C在圆O上,延长BC到D使BC=CD,过C作圆O的切线交AD于E,若AB=8,DC=4,则DE=( )| A. | $\sqrt{2}$ | B. | 2 | C. | $\frac{{2\sqrt{3}}}{3}$ | D. | $\frac{4}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{5}$ | B. | 3 | C. | $\sqrt{13}$ | D. | $\sqrt{17}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com