
【题目】已知四棱锥![]() 的底面为直角梯形
的底面为直角梯形![]() ,
,![]() ,
,![]()
![]() ,
,![]() 是以
是以![]() 为底边的等腰直角三角形.
为底边的等腰直角三角形.

(1)求证:![]() ;
;
(2)若![]() 为
为![]() 的垂心,求二面角
的垂心,求二面角![]() 的余弦值.
的余弦值.
科目:高中数学 来源: 题型:
【题目】《汉字听写大会》不断创收视新高,为了避免“书写危机”弘扬传统文化,某市对全市一定年龄的市民进行了汉字听写测试.为了调查被测试市民的基本情况,组织方从参加测试的市民中随机抽取120名市民,按他们的年龄分组:第一组![]() ,第2组
,第2组![]() ,第3组
,第3组![]() ,第4组
,第4组![]() ,第5组
,第5组![]() ,得到的频率分布直方图如图所示.
,得到的频率分布直方图如图所示.

(1)若电视台记者要从抽取的市民中选1人进行采访,求被采访人恰好在第1组或第4组的概率;
(2)已知第1组市民中男性有3名,组织方要从第1组中随机抽取2名市民组成弘扬传统文化宣传队,求至少有1名女性群众的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱锥![]() 中,平面
中,平面![]() 平面
平面![]() ,
,![]() ,
,![]() ,若
,若![]() 为
为![]() 的中点.
的中点.
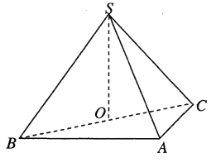
(1)证明:![]() 平面
平面![]() ;
;
(2)求异面直线![]() 和
和![]() 所成角;
所成角;
(3)设线段![]() 上有一点
上有一点![]() ,当
,当![]() 与平面
与平面![]() 所成角的正弦值为
所成角的正弦值为![]() 时,求
时,求![]() 的长.
的长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校实行选科走班制度,张毅同学的选择是物理、生物、政治这三科,且物理在![]() 层班级,生物在
层班级,生物在![]() 层班级.该校周一上午选科走班的课程安排如下表所示,张毅选择三个科目的课各上一节,另外一节上自习,则他不同的选课方法有( )
层班级.该校周一上午选科走班的课程安排如下表所示,张毅选择三个科目的课各上一节,另外一节上自习,则他不同的选课方法有( )
第一节 | 第二节 | 第三节 | 第四节 |
地理 | 化学 | 地理 | 化学 |
生物 | 化学 | 生物 | 历史 |
物理 | 生物 | 物理 | 生物 |
物理 | 生物 | 物理 | 物理 |
政治1班 | 物理 | 政治2班 | 政治3班 |
A.8种B.10种C.12种D.14种
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为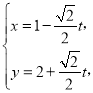 (
(![]() 为参数),以原点
为参数),以原点![]() 为极点,
为极点,![]() 轴为极轴的极坐标系中,圆
轴为极轴的极坐标系中,圆![]() 的方程
的方程![]() .
.
(1)写出直线![]() 的普通方程和圆
的普通方程和圆![]() 的直角坐标方程;
的直角坐标方程;
(2)若点![]() 的直角坐标为
的直角坐标为![]() ,圆
,圆![]() 与直线
与直线![]() 交于
交于![]() 两点,求弦
两点,求弦![]() 中点
中点![]() 的直角坐标和
的直角坐标和![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线C的顶点在原点,对称轴是x轴,并且经过点![]() ,抛物线C的焦点为F,准线为l.
,抛物线C的焦点为F,准线为l.
(1)求抛物线C的方程;
(2)过F且斜率为![]() 的直线h与抛物线C相交于两点A、B,过A、B分别作准线l的垂线,垂足分别为D、E,求四边形
的直线h与抛物线C相交于两点A、B,过A、B分别作准线l的垂线,垂足分别为D、E,求四边形![]() 的面积.
的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com