
【题目】已知正方形的中点为直线![]() 和
和![]() 的交点,正方形一边所在直线的方程为
的交点,正方形一边所在直线的方程为![]() ,求其他三边所在直线的方程.
,求其他三边所在直线的方程.
【答案】解: ![]() ∴中点坐标为M(-1,0)
∴中点坐标为M(-1,0)
点M到直线![]() 的距离
的距离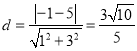
设与![]() 的直线方程为
的直线方程为![]()
![]()
∴![]() (舍)或
(舍)或![]() ∴
∴![]()
设与![]() 垂直两线分别为
垂直两线分别为![]() ,则(-1,0)到这两条直线距离相等且为
,则(-1,0)到这两条直线距离相等且为![]() ,
,
设方程为![]()
∴![]() ∴
∴![]() 或9 ∴
或9 ∴![]()
【解析】设与直线l:x+3y-5=0平行的边的直线方程为l1:x+3y+c=0.
由![]() 得正方形的中心为P(-1,0),由点P到两直线l,l1的距离相等,得
得正方形的中心为P(-1,0),由点P到两直线l,l1的距离相等,得![]() ,解得c=7或c=-5(舍去).
,解得c=7或c=-5(舍去).
∴l1:x+3y+7=0.又∵正方形另两边所在直线与l垂直,
∴设另两边方程为3x-y+a=0,3x-y+b=0.
∵正方形中心到四条边的距离相等,∴![]() ,得a=9或-3,
,得a=9或-3,
∴另两条边所在的直线方程为3x-y+9=0,3x-y-3=0.
∴另三边所在的直线方程分别为3x-y+9=0,x+3y+7=0,3x-y-3=0.


 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案 名师指导一卷通系列答案
名师指导一卷通系列答案科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P-ABCD中,AB∥CD,AB⊥AD,CD=2AB,平面PAD⊥底面ABCD,PA⊥AD.E和F分别是CD和PC的中点,求证:

(1)PA⊥底面ABCD;
(2)平面BEF⊥平面PCD.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)= ![]() ,x∈[-1,1],函数g(x)=[f(x)]2-2af(x)+3的最小值为h(a).
,x∈[-1,1],函数g(x)=[f(x)]2-2af(x)+3的最小值为h(a).
(1)求h(a).
(2)是否存在实数m>n>3,当h(a)的定义域为[n,m]时,值域为[n2,m2]?若存在,求出m,n的值;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下表提供了某厂节能降耗技术改造后生产甲产品过程中记录的产量x(吨)与相应的生产能耗y(吨标准煤)的几组对照数据.
x | 3 | 4 | 5 | 6 |
y | 2.5 | 3 | 4 | 4.5 |
(1)请画出上表数据的散点图.
(2)请根据上表提供的数据,用最小二乘法求出y关于x的线性回归方程![]() .
.
(3)已知该厂技改前100吨甲产品的生产能耗为90吨标准煤.试根据(2)求出的线性回归方程,预测生产100吨甲产品的生产能耗比技改前降低多少吨标准煤.
(参考数值:3×2.5+4×3+5×4+6×4.5=66.5)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知在平行四边形ABCD中,A(1,2),B(2,1),中心E(3,3).
(1)判断平行四边形ABCD是否为正方形;
(2)点P(x,y)在平行四边形ABCD的边界及内部运动,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x2+alnx(a为实常数)
(1)若a=﹣2,求证:函数f(x)在(1,+∞)上是增函数;
(2)求函数f(x)在[1,e]上的最小值及相应的x值;
(3)若存在x∈[1,e],使得f(x)≤(a+2)x成立,求实数a的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com