
【题目】如图,![]() 是边长为2的正方形,
是边长为2的正方形,![]() 平面
平面![]() ,且
,且![]() .
.
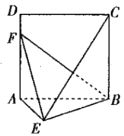
(Ⅰ)求证:平面![]() 平面
平面![]() ;
;
(Ⅱ)线段![]() 上是否存在一点
上是否存在一点![]() ,使二而角
,使二而角![]() 等于45°?若存在,请找出点
等于45°?若存在,请找出点![]() 的位置;若不存在,请说明理由.
的位置;若不存在,请说明理由.
 口算题天天练系列答案
口算题天天练系列答案科目:高中数学 来源: 题型:
【题目】在平面直角坐标点xOy中,以坐标原点为极点,x轴正半轴为极轴建立极坐标系,曲线C1的极坐标方程为ρsinθ=6.
(1)A为曲线C1上的动点,点M在线段OA上,且满足|OM||OA|=36,求点M的轨迹C2的直角坐标方程;
(2)点E的极坐标为(4,![]() ),点F在曲线C2上,求△OEF面积的最大值
),点F在曲线C2上,求△OEF面积的最大值
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列![]() 的前
的前![]() 项和为
项和为![]() ,且满足
,且满足![]() ,
,![]() ,设
,设![]() ,
,![]() .
.
(Ⅰ)求证:数列![]() 是等比数列;
是等比数列;
(Ⅱ)若![]() ,
,![]() ,求实数
,求实数![]() 的最小值;
的最小值;
(Ⅲ)当![]() 时,给出一个新数列
时,给出一个新数列![]() ,其中
,其中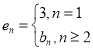 ,设这个新数列的前
,设这个新数列的前![]() 项和为
项和为![]() ,若
,若![]() 可以写成
可以写成![]() (
(![]() ,
,![]() 且
且![]() ,
,![]() )的形式,则称
)的形式,则称![]() 为“指数型和”.问
为“指数型和”.问![]() 中的项是否存在“指数型和”,若存在,求出所有“指数型和”;若不存在,请说明理由.
中的项是否存在“指数型和”,若存在,求出所有“指数型和”;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为:
的参数方程为:![]() (
(![]() 为参数),以平面直角坐标系的原点
为参数),以平面直角坐标系的原点![]() 为极点,
为极点,![]() 轴的非负半轴为极轴建立极坐标系,将曲线
轴的非负半轴为极轴建立极坐标系,将曲线![]() 绕极点顺时针旋转
绕极点顺时针旋转![]() 后得到曲线的曲线记为
后得到曲线的曲线记为![]() .
.
(1)求曲线![]() 和
和![]() 的极坐标方程;
的极坐标方程;
(2)设![]() 和
和![]() 的交点为
的交点为![]() ,
,![]() ,求
,求![]() 的长度.
的长度.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为响应党中央“扶贫攻坚”的号召,某单位指导一贫困村通过种植紫甘薯来提高经济收入.紫甘薯对环境温度要求较高,根据以往的经验,随着温度的升高,其死亡株数成增长的趋势.下表给出了2017年种植的一批试验紫甘薯在温度升高时6组死亡的株数:

经计算: ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,其中
,其中![]() 分别为试验数据中的温度和死亡株数,
分别为试验数据中的温度和死亡株数, ![]() .
.
(1)若用线性回归模型,求![]() 关于
关于![]() 的回归方程
的回归方程![]() (结果精确到
(结果精确到![]() );
);
(2)若用非线性回归模型求得![]() 关于
关于![]() 的回归方程为
的回归方程为![]() ,且相关指数为
,且相关指数为![]() .
.
(i)试与(1)中的回归模型相比,用![]() 说明哪种模型的拟合效果更好;
说明哪种模型的拟合效果更好;
(ii)用拟合效果好的模型预测温度为![]() 时该批紫甘薯死亡株数(结果取整数).
时该批紫甘薯死亡株数(结果取整数).
附:对于一组数据![]() ,
, ![]() ,……,
,……, ![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘估计分别为:
的斜率和截距的最小二乘估计分别为:  ;相关指数为:
;相关指数为:  .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我国古代著名数学家刘徽的杰作《九章算术注》是中国最宝贵的数学遗产之一,书中记载了他计算圆周率所用的方法.先作一个半径为1的单位圆,然后做其内接正六边形,在此基础上做出内接正![]() 边形,这样正多边形的边逐渐逼近圆周,从而得到圆周率,这种方法称为“刘徽割圆术”.现设单位圆
边形,这样正多边形的边逐渐逼近圆周,从而得到圆周率,这种方法称为“刘徽割圆术”.现设单位圆![]() 的内接正
的内接正![]() 边形的一边为
边形的一边为![]() ,点
,点![]() 为劣弧
为劣弧![]() 的中点,则
的中点,则![]() 是内接正
是内接正![]() 边形的一边,现记
边形的一边,现记![]() ,
,![]() ,则( )
,则( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对于某种类型的口服药,口服![]() 小时后,由消化系统进入血液中药物浓度
小时后,由消化系统进入血液中药物浓度![]() (单位)与时间
(单位)与时间![]() 小时的关系为
小时的关系为![]() ,其中
,其中![]() ,
,![]() 为常数,对于某一种药物
为常数,对于某一种药物![]() ,
,![]() ,
,![]() .
.
(1)口服药物后______小时血液中药物浓度最高;
(2)这种药物服药![]() 小时后血液中药物浓度如下表
小时后血液中药物浓度如下表
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 0.9545 | 0.9304 | 0.6932 | 0.4680 | 0.3010 | 0.1892 | 0.1163 | 0.072 |
一个病人上午8:00第一次服药,要使得病人血液中药物浓度保持在0.5个单位以上,第三次服药时间是______(时间以整点为准)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() (
(![]() ,且
,且![]() 为常数).
为常数).
(1)若函数![]() 的图象在
的图象在![]() 处的切线的斜率为
处的切线的斜率为![]() (
(![]() 为自然对数的底数),求
为自然对数的底数),求![]() 的值;
的值;
(2)若函数![]() 在区间
在区间![]() 上单调递增,求
上单调递增,求![]() 的取值范围;
的取值范围;
(3)已知![]() ,且
,且![]() .求证:
.求证:![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com