
如图,焦距为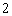 的椭圆
的椭圆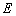 的两个顶点分别为
的两个顶点分别为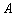 和
和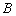 ,且
,且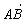 与n
与n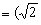 ,
,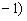 共线.
共线.

(1)求椭圆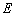 的标准方程;
的标准方程;
(2)若直线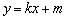 与椭圆
与椭圆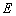 有两个不同的交点
有两个不同的交点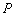 和
和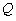 ,且原点
,且原点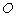 总在以
总在以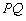 为直径的圆的内部,
为直径的圆的内部,
求实数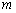 的取值范围.
的取值范围.
(1) 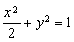 ;(2)
;(2)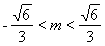 .
.
【解析】
试题分析:(1)根据椭圆方程写出顶点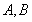 的坐标,然后写出
的坐标,然后写出 的坐标,利用两向量共线的充要条件:
的坐标,利用两向量共线的充要条件: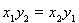 ,得
,得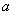 与
与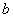 的关系,结合
的关系,结合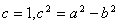 ,解出
,解出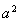 与
与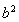 ,求出椭圆的方程;(2)设直线
,求出椭圆的方程;(2)设直线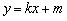 ,与椭圆
,与椭圆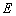 有两个不同的交点
有两个不同的交点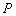 和
和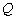 ,设
,设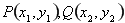 ,将直线方程代入椭圆方程,消去
,将直线方程代入椭圆方程,消去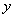 ,得到关于
,得到关于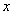 的方程,由两个不同交点,
的方程,由两个不同交点, ,并且得到
,并且得到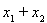 与
与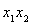 ,
, 原点
原点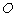 总在以
总在以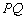 为直径的圆的内部,
为直径的圆的内部,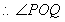 为钝角,即
为钝角,即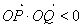 ,整理,代入根与系数的关系,比较
,整理,代入根与系数的关系,比较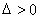 得出
得出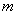 的取值范围.
的取值范围.
试题解析:(1)解:设椭圆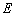 的标准方程为
的标准方程为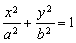
 ,由已知得
,由已知得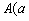 ,
,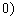 ,
,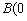 ,
,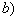 ,所以
,所以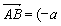 ,
,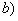 ,
,
因为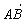 与n
与n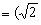 ,
,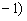 共线,所以
共线,所以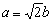 , 2分
, 2分
由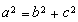 ,解得
,解得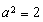 ,
,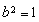 ,
,
所以椭圆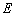 的标准方程为
的标准方程为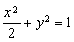 . 4分
. 4分
(2)解:设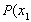 ,
,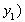 ,
,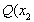 ,
,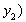 ,把直线方程
,把直线方程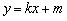 代入椭圆方程
代入椭圆方程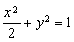 ,
,
消去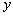 ,得
,得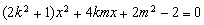 ,
,
所以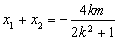 ,
,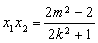 , 8分
, 8分
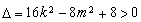 ,即
,即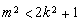 (*) 9分
(*) 9分
因为原点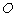 总在以
总在以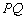 为直径的圆的内部,
为直径的圆的内部,
所以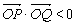 ,即
,即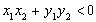 , 10分
, 10分
又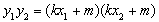
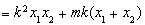
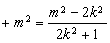 ,
,
由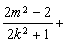
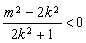 得
得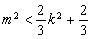 , 13分
, 13分
依题意且满足(*)得 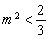
故实数 的取值范围是
的取值范围是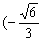 ,
,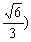 . 14分
. 14分
考点:1.椭圆的性质与方程;2.向量共线的充要条件;3.直线与椭圆相交.


科目:高中数学 来源: 题型:
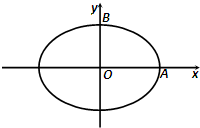 (2012•河南模拟)如图,焦距为2的椭圆E的两个顶点分别为A和B,且
(2012•河南模拟)如图,焦距为2的椭圆E的两个顶点分别为A和B,且| AB |
| n |
| 2 |
查看答案和解析>>
科目:高中数学 来源:2013-2014学年天津河西区高三第一学期形成性质量调查理科数学试卷(解析版) 题型:解答题
如图,焦距为 的椭圆
的椭圆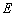 的两个顶点分别为
的两个顶点分别为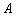 和
和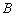 ,且
,且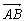 与n
与n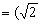 ,
,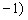 共线.
共线.

(1)求椭圆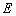 的标准方程;
的标准方程;
(2)若直线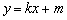 与椭圆
与椭圆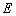 有两个不同的交
有两个不同的交
点 和
和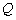 ,且原点
,且原点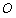 总在以
总在以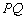 为直径的圆的内部,求实数
为直径的圆的内部,求实数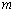 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源:2012-2013学年河北省邯郸市磁县一中高二(下)期中数学试卷(理科)(实验部)(解析版) 题型:解答题
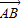 与
与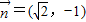 共线.
共线.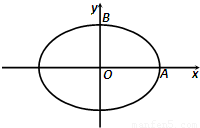
查看答案和解析>>
科目:高中数学 来源:2012-2013学年福建省福州市泉港二中高三(上)第11周周考数学试卷(理科)(解析版) 题型:解答题
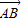 与
与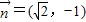 共线.
共线.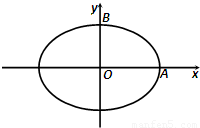
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com