
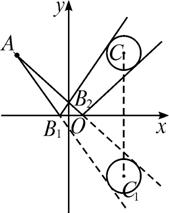
【探究】 (1)如图所示,设l和x轴交于B(b,0),则kAB=![]() ,根据光的反射定律,反射线的斜率k反=
,根据光的反射定律,反射线的斜率k反=![]() ,
,
∴反射线所在的直线方程为
y=![]() (x-b).
(x-b).
即 3x-(b+3)y-3b=0.
∵已知圆x2+y2-4x-4y+7=0的圆心为C(2,2),半径为1,
∴![]() .解得b1=
.解得b1=![]() ,b2=1.
,b2=1.
∴kAB=![]() 或kAB=
或kAB=![]() .
.
∴l的方程为4x+3y+3=0或3x+4y-3=0.
(2)已知圆C:x2+y2-4x-4y+7=0关于x轴对称的圆为C1:(x-2)2+(y+2)2=1,其圆心C1的坐标为(2,-2),半径为1,由光的反射定律知,入射光线所在直线方程与圆C1相切.
设l的方程为y-3=k(x+3),则![]() ,
,
即 12k2+25k+12=0.∴k1=![]() ,k2=
,k2=![]() .
.
则l的方程为4x+3y+3=0或3x+4y-3=0.
(3)设入射光线方程为y-3=k(x+3),反射光线所在直线方程为y=-kx+b,由于二者横截距相等,且后者与已知圆相切,
∴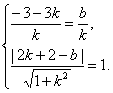
消去b得![]() =1(以下与解析(2)同).
=1(以下与解析(2)同).
【规律总结】 本题是方程思想的典型应用,考查的重点在于设置怎样的未知数,依怎样的性质列方程,解析(1)、(2)属常规方法,解析(3)设置两个未知数,体现了方程的方法在具体运用时的灵活性.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
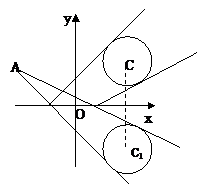
自点A(-3,3)发出的光线L射到x轴上,被x轴反射,其反射光线m所在直线与圆C:x 2 + y 2 -4x-4y +7 = 0相切,求光线L、m所在的直线方程.
查看答案和解析>>
科目:高中数学 来源:2011-2012学年四川省汉源县第一中学高二上学期期中理科数学试卷 题型:解答题
自点A(-3,3)发出的光线L射到x轴上,被x轴反射,其反射光线所在直线与圆x2+y2-4x-4y+7=0相切,求光线L所在直线的方程。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com