
分析 由向量垂直数量积为0,利用题设条件,能求出λ的值.
解答 解:∵向量$λ\overrightarrow a-\overrightarrow b$与$\overrightarrow a+2\overrightarrow b$互相垂直,
∴($λ\overrightarrow a-\overrightarrow b$)($\overrightarrow a+2\overrightarrow b$)=0,即λ${\overrightarrow{a}}^{2}$+(2λ-1)$\overrightarrow{a}$•$\overrightarrow{b}$-2${\overrightarrow{b}}^{2}$=λ-8+(2λ-1)×1×2×$\frac{1}{2}$=0,
解得λ=3.
故答案是:3.
点评 本题考查向量的模的求法,考查向量垂直的条件的应用,是基础题,解题时要熟练掌握向量的数量积的运算.


 学练快车道快乐假期寒假作业系列答案
学练快车道快乐假期寒假作业系列答案 新思维寒假作业系列答案
新思维寒假作业系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{3}{4}$ | B. | $\frac{2}{3}$ | C. | $\frac{3}{5}$ | D. | $\frac{1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $(\frac{π}{4},\frac{π}{2})∪(π,\frac{5}{4}π)$ | B. | $(\frac{π}{4},π)$ | C. | $(\frac{π}{4},\frac{3}{4}π)∪(\frac{5π}{4},\frac{7}{4}π)$ | D. | $(\frac{π}{4},\frac{π}{2})∪(\frac{5}{4}π,\frac{3}{2}π)$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ${[{1-{{({\frac{5}{6}})}^{10}}}]^5}$ | B. | ${[{1-{{({\frac{5}{6}})}^6}}]^{10}}$ | C. | 1 $-{[{1-{{({\frac{1}{6}})}^5}}]^{10}}$ | D. | 1$-{[{1-{{({\frac{1}{6}})}^{10}}}]^5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -$\frac{1}{{2}^{n}}$$\frac{(-1)^{n}}{{2}^{n}}$ | B. | $\frac{(-1)^{n}}{{2}^{n}}$ | C. | $\frac{(-1)^{n+1}}{{2}^{n}}$ | D. | $\frac{(-1)^{n}}{{2}^{n-1}}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
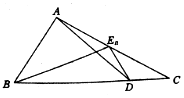 如图,已知点D为△ABC的边BC上一点,$\overrightarrow{BD}$=3$\overrightarrow{DC}$,En(n∈N+)为边AC的一列点,满足$\overrightarrow{{E}_{n}A}$=$\frac{1}{4}$an+1$\overrightarrow{{E}_{n}B}$-(3an+2)$\overrightarrow{{E}_{n}D}$,其中实数列{an}中an>0,a1=1,则{an}的通项公式为( )
如图,已知点D为△ABC的边BC上一点,$\overrightarrow{BD}$=3$\overrightarrow{DC}$,En(n∈N+)为边AC的一列点,满足$\overrightarrow{{E}_{n}A}$=$\frac{1}{4}$an+1$\overrightarrow{{E}_{n}B}$-(3an+2)$\overrightarrow{{E}_{n}D}$,其中实数列{an}中an>0,a1=1,则{an}的通项公式为( )| A. | 3•2n-1-2 | B. | 2n-1 | C. | 3n-2 | D. | 2•3n-1-1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com