
分析 (1)利用椭圆的定义,求轨迹C的方程;
(2)若直线l:y=kx+m与曲线C交于不同的两点A,B,与圆x2+y2=1相切于点M.
①证明x1x2+y1y2=$\frac{3{m}^{2}-3({k}^{2}+1)}{2{k}^{2}+1}$=0,即可证明:OA⊥OB(O为坐标原点);
②λ=$\frac{|AM|}{|BM|}$=$\frac{\sqrt{{{x}_{1}}^{2}+1}}{\sqrt{{{x}_{2}}^{2}+1}}$,(Ⅱ)①知x1x2+y1y2=0,x1x2=-y1y2,即${{x}_{2}}^{2}$=$\frac{3-{{x}_{1}}^{2}}{{{x}_{2}}^{2}+1}$.λ=$\frac{\sqrt{{{x}_{1}}^{2}+1}}{\sqrt{{{x}_{2}}^{2}+1}}$=$\frac{{{x}_{1}}^{2}+1}{2}$,即可求实数λ的取值范围.
解答 解:(1)由题意,$\sqrt{(x-\frac{\sqrt{6}}{2})^{2}+{y}^{2}}$,$\sqrt{3}$,$\sqrt{(x+\frac{\sqrt{6}}{2})^{2}+{y}^{2}}$成等差数列,
∴$\sqrt{(x-\frac{\sqrt{6}}{2})^{2}+{y}^{2}}$+$\sqrt{(x+\frac{\sqrt{6}}{2})^{2}+{y}^{2}}$=2$\sqrt{3}$,
∴C的轨迹是以(-$\frac{\sqrt{6}}{2}$,0),($\frac{\sqrt{6}}{2}$,0)为焦点,2$\sqrt{3}$为长轴长的椭圆,
∴a=$\sqrt{3}$,b=$\frac{\sqrt{6}}{2}$,
∴椭圆C的方程为$\frac{{x}^{2}}{3}+\frac{2{y}^{2}}{3}$=1;
(2)①证明:∵直线l:y=kx+m与圆x2+y2=1相切,
∴d=$\frac{|m|}{\sqrt{1+{k}^{2}}}$=1,即m2=k2+1,
由直线代入椭圆方程,消去y并整理得,(1+2k2)x2+4kmx+2m2-3=0.
设A(x1,y1),B(x2,y2),∴x1+x1=-$\frac{4km}{1+2{k}^{2}}$,x1x2=$\frac{2{m}^{2}-3}{1+2{k}^{2}}$
∴x1x2+y1y2=$\frac{3{m}^{2}-3({k}^{2}+1)}{2{k}^{2}+1}$=0,
∴OA⊥OB;
②∵直线l:y=kx+m与椭圆交于不同的两点A,B,
∴$\frac{{{x}_{1}}^{2}}{3}+\frac{2{{y}_{1}}^{2}}{3}$=1,$\frac{{{x}_{2}}^{2}}{3}+\frac{2{{y}_{2}}^{2}}{3}=1$.
∴λ=$\frac{|AM|}{|BM|}$=$\frac{\sqrt{{{x}_{1}}^{2}+1}}{\sqrt{{{x}_{2}}^{2}+1}}$,
由(2)①知x1x2+y1y2=0,
∴x1x2=-y1y2,即x12x22=y12y22=$\frac{1}{2}$(3-x12)•$\frac{1}{2}$(3-x22),
即有${{x}_{2}}^{2}$=$\frac{3-{{x}_{1}}^{2}}{{{x}_{1}}^{2}+1}$.
∴λ=$\frac{\sqrt{{{x}_{1}}^{2}+1}}{\sqrt{{{x}_{2}}^{2}+1}}$=$\frac{{{x}_{1}}^{2}+1}{2}$
∵$-\sqrt{3}≤{x}_{1}≤\sqrt{3}$,
∴λ的取值范围是$\frac{1}{2}≤λ≤2$.
点评 本题考查椭圆的简单性质,考查了直线与圆、圆与椭圆位置关系的应用,训练了利用向量数量积判断两条线段的垂直关系,考查运算能力,属难题.


 通城学典默写能手系列答案
通城学典默写能手系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,1) | B. | (1,+∞) | C. | (0,1) | D. | (1,2) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | $\frac{9}{4}$ | C. | 4 | D. | $\frac{9}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
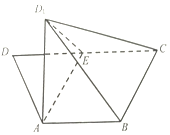 已知四边形ABCD中,AB∥CD,AD=AB=BC=$\frac{1}{2}$CD=2,E为DC中点,连接AE,将△DAE沿AE翻折到△D1AE.
已知四边形ABCD中,AB∥CD,AD=AB=BC=$\frac{1}{2}$CD=2,E为DC中点,连接AE,将△DAE沿AE翻折到△D1AE.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
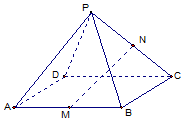 如图,在四棱锥P-ABCD中,M,N分别是AB,PC的中点,若ABCD是平行四边形.
如图,在四棱锥P-ABCD中,M,N分别是AB,PC的中点,若ABCD是平行四边形.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com