【题目】某工厂今年前三个月生产某种产品的数量统计表如下：
为了估测以后每个月的产量，以这三个月的产量为依据，用一个函数模拟产品的月产量
与月份
的关系，模拟函数可选择二次函数
（
为常数且
），或函数
（
为常数）.已知4月份的产量为1.37万件，请问用以上哪个函数作为模拟函数较好，请说明理由.
科目：高中数学 来源： 题型：
【题目】已知
，若
，且
的图象相邻的对称轴间的距离不小于
.
（1）求
的取值范围.
（2）若当
取最大值时， 
，且在
中， 
分别是角
的对边，其面积
，求
周长的最小值.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】唐三彩，中国古代陶瓷烧制工艺的珍品，它吸取了中国国画、雕塑等工艺美术的特点，在中国文化中占有重要的历史地位，在中国的陶瓷史上留下了浓墨重彩的一笔.唐三彩的生产至今已有1300多年的历史，对唐三彩的复制和仿制工艺，至今也有百余年的历史，某陶瓷厂在生产过程中，对仿制的100件工艺品测得其重量（单位： 
）数据，将数据分组如下表：
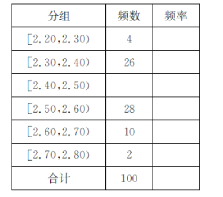
（1）在答题卡上完成频率分布表；
（2）以表中的频率作为概率，估计重量落在
中的概率及重量小于2.45的概率是多少？
（3）统计方法中，同一组数据常用该组区间的中点值（例如区间
的中点值是2.25作为代表.据此，估计这100个数据的平均值.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】甲、乙两位学生参加数学竞赛培训．现分别从他们在培训期间参加的若干次预赛成绩中随机抽取
次．记录如下：
甲： 
， 
， 
， 
， 
， 
， 
， 
乙： 
， 
， 
， 
， 
， 
， 
， 
（
）用茎叶图表示这两组数据．
（
）现要从中选派一人参加数学竞赛，从统计学的角度考虑，你认为派哪位学生参加合适?请说明理由．
（
）若将频率视为概率，对甲同学在今后的三次数学竞赛成绩进行预测，记这
次成绩中高于
分的次数为
，求
的分布列及数学期望．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知函数
(1)求函数
在区间
上的值域
(2)把函数图象所有点的上横坐标缩短为原来的
倍，再把所得的图象向左平移
个单位长度
，再把所得的图象向下平移1个单位长度，得到函数
， 若函数关于点
对称
（i）求函数的解析式；
（ii）求函数单调递增区间及对称轴方程.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】某市甲水厂每天生产
万吨的生活用水，其每天固定生产成本为
万元，居民用水的税费价格为每吨
元，该市居民每天用水需求量是在
（单位：万吨）内的随机数，经市场调查，该市每天用水需求量的频率分布直方图如图所示，设
（单位：万吨， 
）表示该市一天用水需求量
（单位：万元）表示甲水厂一天销售生活用水的利润（利润=税费收入-固定生产成本），注：当该市用水需求量超过
万吨时，超过的部分居民可以用其他水厂生产的水，甲水厂只收成本厂供应的税费，该市每天用水需求量的概率用频率估计.
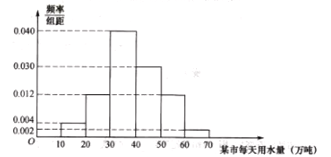
（1）求
的值，并直接写出
表达式；
（2）求甲水厂每天的利润不少于
万元的概率.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】以下四个关于圆锥曲线的命题：
①设A，B是两个定点，k为非零常数，若|PA|－|PB|＝k，则P的轨迹是双曲线；
②过定圆C上一定点A作圆的弦AB，O为原点，若
．则动点P的轨迹是椭圆；
③方程
的两根可以分别作为椭圆和双曲线的离心率；
④双曲线
与椭圆
有相同的焦点．
其中正确命题的序号为________．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】2018年1月8日，中共中央国务院隆重举行国家科学技术奖励大会，在科技界引发热烈反响，自主创新正成为引领经济社会发展的强劲动力.某科研单位在研发新产品的过程中发现了一种新材料，由大数据测得该产品的性能指标值y与这种新材料的含量x（单位：克）的关系为：当
时，y是x的二次函数；当
时，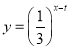
测得数据如下表（部分）：
x（单位：克） | 0 | 1 | 2 | 9 | … |
y | 0 |
| 3 |
| … |
（1）求y关于x的函数关系式
；
（2）当该产品中的新材料含量x为何值时，产品的性能指标值最大.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
