
【题目】已知抛物线![]() 与斜率为
与斜率为![]() 且过抛物线焦点
且过抛物线焦点![]() 的直线
的直线![]() 交于
交于![]() 、
、![]() 两点,满足弦长
两点,满足弦长![]() .
.
(1)求抛物线的标准方程;
(2)已知![]() 为抛物线上任意一点,
为抛物线上任意一点,![]() 为抛物线内一点,求
为抛物线内一点,求![]() 的最小值,以及此时点
的最小值,以及此时点![]() 的坐标.
的坐标.
 开心蛙状元测试卷系列答案
开心蛙状元测试卷系列答案科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在平面直角坐标系![]() 中,以坐标原点
中,以坐标原点![]() 为极点,
为极点, ![]() 轴正半轴为极轴建立极坐标系,已知曲线
轴正半轴为极轴建立极坐标系,已知曲线![]() 的极坐标方程为:
的极坐标方程为: ![]() ,直线
,直线![]() 的参数方程是
的参数方程是![]() (
(![]() 为参数,
为参数, ![]() ).
).
(1)求曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)设直线![]() 与曲线
与曲线![]() 交于两点
交于两点![]() ,且线段
,且线段![]() 的中点为
的中点为![]() ,求
,求![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,五边形![]() 中,四边形
中,四边形![]() 为长方形,
为长方形,![]() 为边长为
为边长为![]() 的正三角形,将
的正三角形,将![]() 沿
沿![]() 折起,使得点
折起,使得点![]() 在平面
在平面![]() 上的射影恰好在
上的射影恰好在![]() 上.
上.
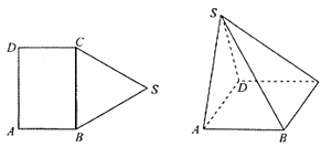
(Ⅰ)当![]() 时,证明:平面
时,证明:平面![]() 平面
平面![]() ;
;
(Ⅱ)若![]() ,求平面
,求平面![]() 与平面
与平面![]() 所成二面角的余弦值的绝对值.
所成二面角的余弦值的绝对值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线的顶点在原点,焦点![]() 在
在![]() 轴的正半轴,且过点
轴的正半轴,且过点![]() ,过
,过![]() 的直线交抛物线于
的直线交抛物线于![]() ,
,![]() 两点.
两点.
(1)求抛物线的方程;
(2)设直线![]() 是抛物线的准线,求证:以
是抛物线的准线,求证:以![]() 为直径的圆与直线
为直径的圆与直线![]() 相切.
相切.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在中老年人群体中,肠胃病是一种高发性疾病某医学小组为了解肠胃病与运动之间的联系,调查了50位中老年人每周运动的总时长(单位:小时),将数据分成[0,4),[4,8),[8,14),[14,16),[16,20),[20,24]6组进行统计,并绘制出如图所示的柱形图.
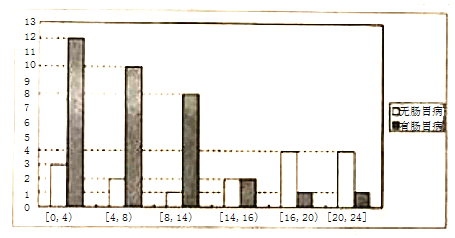
图中纵轴的数字表示对应区间的人数现规定:每周运动的总时长少于14小时为运动较少.
每周运动的总时长不少于14小时为运动较多.
(1)根据题意,完成下面的2×2列联表:
有肠胃病 | 无肠胃病 | 总计 | |
运动较多 | |||
运动较少 | |||
总计 |
(2)能否有99.9%的把握认为中老年人是否有肠胃病与运动有关?
附:K2 (n=a+b+c+d)
(n=a+b+c+d)
P(K2≥k) | 0.0.50 | 0.010 | 0.001 |
k | 3.841 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线![]() , (
, (![]() 为参数,
为参数, ![]() 为倾斜角).以坐标原点为极点,
为倾斜角).以坐标原点为极点, ![]() 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线![]() 的直角坐标方程为
的直角坐标方程为![]() .
.
(Ⅰ)将曲线![]() 的直角坐标方程化为极坐标方程;
的直角坐标方程化为极坐标方程;
(Ⅱ)设点![]() 的直角坐标为
的直角坐标为![]() ,直线
,直线![]() 与曲线
与曲线![]() 的交点为
的交点为![]() 、
、![]() ,求
,求![]() 的取值范围.
的取值范围.
【答案】(I)![]() ;(II)
;(II)![]() .
.
【解析】试题分析:(Ⅰ)将由![]() 代入
代入![]() ,化简即可得到曲线
,化简即可得到曲线![]() 的极坐标方程;(Ⅱ)将
的极坐标方程;(Ⅱ)将![]() 的参数方程
的参数方程![]() 代入
代入![]() ,得
,得![]() ,根据直线参数方程的几何意义,利用韦达定理结合辅助角公式,由三角函数的有界性可得结果.
,根据直线参数方程的几何意义,利用韦达定理结合辅助角公式,由三角函数的有界性可得结果.
试题解析:(Ⅰ)由![]() 及
及![]() ,得
,得![]() ,即
,即![]()
所以曲线![]() 的极坐标方程为
的极坐标方程为![]()
(II)将![]() 的参数方程
的参数方程![]() 代入
代入![]() ,得
,得![]()
∴ , 所以
, 所以![]() ,又
,又![]() ,
,
所以![]() ,且
,且![]() ,
,
所以![]() ,
,
由![]() ,得
,得![]() ,所以
,所以![]() .
.
故![]() 的取值范围是
的取值范围是![]() .
.
【题型】解答题
【结束】
23
【题目】已知![]() 、
、![]() 、
、![]() 均为正实数.
均为正实数.
(Ⅰ)若![]() ,求证:
,求证: ![]()
(Ⅱ)若![]() ,求证:
,求证: ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com