
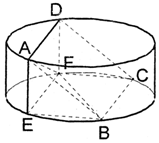
 如图,圆柱的高为2,底面半径为3,AE,DF是圆柱的两条母线,B、C是下底面圆周上的两点,已知四边形ABCD是正方形.
如图,圆柱的高为2,底面半径为3,AE,DF是圆柱的两条母线,B、C是下底面圆周上的两点,已知四边形ABCD是正方形.分析 (1)根据AE⊥底面BEFC,可得AE⊥BC,而AB⊥BC,又AE∩AB=A满足线面垂直的判定定理所需条件,则BC⊥面ABE,根据线面垂直的性质可知BC⊥BE;.
(2)根据题意可知四边形EFBC为矩形则BF为圆柱下底面的直径,设正方形ABCD的边长为x,建立方程,解之即可求出经,由此能求出几何体AEB-DFC的体积.
(3)以F为原点建立空间直角坐标系,利用向量法能求出平面DFC与平面ABF所成的锐二面角的余弦值.
解答 证明:(1)∵AE是圆柱的母线,∴AE⊥底面BEFC,
∵BC?面BEFC,∴AE⊥BC,
∵ABCD是正方形,∴AB⊥BC,
又AE∩AB=A,∴BC⊥面ABE,
又BE?面AB,∴BC⊥BE.
(2)∵四边形AEFD为矩形,且ABCD是正方,∴EF$\underset{∥}{=}$BC,
∵BC⊥BE,∴四边形EFBC为矩形,
∴BF为圆柱下底面的直径,
设正方形ABCD的边长为x,则AD=EF=AB=x,
在直角△AEB中,AE=2,AB=x,且BE2+AE2=AB2,得BE2=x2-4,
在直角△BEF中,BF=6,EF=x,且BE2+EF2=BF2,得BE2=36-x2,
解得x=2$\sqrt{5}$,即正方形ABCD的边长为2$\sqrt{5}$,
∴何体AEB-DFC的体积V=S△AEB•EF=$\frac{1}{2}×AE×BE×EF$=$\frac{1}{2}×2×\sqrt{(2\sqrt{5})^{2}-{2}^{2}}×2\sqrt{5}$=8$\sqrt{5}$.
(3)如图以F为原点建立空间直角坐标系,
则A(2$\sqrt{5}$,0,2),B(2$\sqrt{5}$,4,0),F(0,0,0),C(0,4,0),D(0,0,2),
$\overrightarrow{FA}$=(2$\sqrt{5}$,0,2),$\overrightarrow{FB}$=(2$\sqrt{5}$,4,0),$\overrightarrow{FC}$=(0,4,0),$\overrightarrow{FD}$=(0,0,2),
设平面ABF的法向量$\overrightarrow{n}$=(x,y,z),
则$\left\{\begin{array}{l}{\overrightarrow{n}•\overrightarrow{FA}=2\sqrt{5}x+2z=0}\\{\overrightarrow{n}•\overrightarrow{FB}=2\sqrt{5}x+4y=0}\end{array}\right.$,取x=$\sqrt{5}$,得$\overrightarrow{n}$=($\sqrt{5}$,-$\frac{5}{2}$,-5),
设平面CDF的法向量$\overrightarrow{m}$=(1,0,0),
设平面DFC与平面ABF所成的锐二面角为θ,
则cosθ=$\frac{|\overrightarrow{m}•\overrightarrow{n}|}{|\overrightarrow{m}|•|\overrightarrow{n}|}$=$\frac{\sqrt{5}}{\sqrt{\frac{145}{4}}}$=$\frac{2\sqrt{29}}{29}$.
∴平面DFC与平面ABF所成的锐二面角的余弦值为$\frac{2\sqrt{29}}{29}$.
点评 本题主要考查了线线位置关系,线面所成角的度量,以及利用空间向量的方法求解立体几何问题,属于中档题,考查空间想象能力,计算能力.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 等腰直角三角形 | B. | 等边三角形 | C. | 直角三角形 | D. | 钝角三角形 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{3}}{2}$ | C. | $\sqrt{3}$ | D. | $\frac{\sqrt{39}}{26}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ③④ | B. | ①③ | C. | ①② | D. | ②④ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com