
【题目】有两位射击运动员在一次射击测试中各射靶7次,每次命中的环数如下:
甲 7 8 10 9 8 8 6 乙 9 10 7 8 7 7 8
则下列判断正确的是( )
A. 甲射击的平均成绩比乙好 B. 甲射击的成绩的众数小于乙射击的成绩的众数
C. 乙射击的平均成绩比甲好 D. 甲射击的成绩的极差大于乙射击的成绩的极差
科目:高中数学 来源: 题型:
【题目】已知某运动员每次投篮命中的概率低于![]() ,现采用随机模拟的方法估计该运动员三次投篮恰有两次命中的概率:先由计算器产生0到9之间取整数值的随机数,指定1,2,3,4表示命中,5,6,7,8,9,0表示不命中;再以每三个随机数为一组,代表三次投篮的结果,经随机模拟产生了如下20组随机数:
,现采用随机模拟的方法估计该运动员三次投篮恰有两次命中的概率:先由计算器产生0到9之间取整数值的随机数,指定1,2,3,4表示命中,5,6,7,8,9,0表示不命中;再以每三个随机数为一组,代表三次投篮的结果,经随机模拟产生了如下20组随机数:
907 966 191 925 271 932 812 458 569 683
431 257 393 027 556 488 730 113 537 989
据此估计,该运动员三次投篮恰有两次命中的概率为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列结论中:
①定义在R上的函数f(x)在区间(-∞,0]上是增函数,在区间[0,+∞)上也是增函数,则函数f(x)在R上是增函数;②若f(2)=f(-2),则函数f(x)不是奇函数;③函数y=x-0.5是(0,1)上的减函数;④对应法则和值域相同的函数的定义域也相同;⑤若x0是二次函数y=f(x)的零点,且m<x0<n,那么f(m)f(n)<0一定成立.
写出上述所有正确结论的序号:_____.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面四边形ABCD中,AB=BD=CD=1,AB⊥BD,CD⊥BD,将△ABD沿BD折起,使得平面ABD⊥平面BCD,如图. 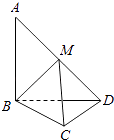
(1)求证:AB⊥CD;
(2)若M为AD中点,求直线AD与平面MBC所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知定义在 R 上的奇函数 f (x) ,设其导函数为 f x ,当 x ,0时,恒有xf x f x 0 ,令 F x xf x,则满足 F(3) F 2x 1 的实数 x 的取值范围是______.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C:x2+2y2=4,
(1)求椭圆C的离心率
(2)设O为原点,若点A在椭圆C上,点B在直线y=2上,且OA⊥OB,求直线AB与圆x2+y2=2的位置关系,并证明你的结论.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲与乙午觉醒来后,发现自己的手表因故停止转动,于是他们想借助收音机,利用电台整点报时确认时间.
(1)求甲等待的时间不多于10分钟的概率;
(2)求甲比乙多等待10分钟以上的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面上, ![]() ⊥
⊥ ![]() ,|
,| ![]() |=|
|=| ![]() |=1,
|=1, ![]() =
= ![]() +
+ ![]() .若|
.若| ![]() |<
|< ![]() ,则|
,则| ![]() |的取值范围是( )
|的取值范围是( )
A.(0, ![]() ]
]
B.( ![]() ,
, ![]() ]
]
C.( ![]() ,
, ![]() ]
]
D.( ![]() ,
, ![]() ]
]
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com