
【题目】已知函数![]() .
.
(1)若![]() 在
在![]() 处与直线
处与直线![]() 相切,求
相切,求![]() 的值;
的值;
(2)在(1)的条件下,求![]() 在
在![]() 上的最大值;
上的最大值;
(3)若不等式![]() 对所有的
对所有的![]() 都成立,求
都成立,求![]() 的取值范围.
的取值范围.
【答案】(1)![]() ;(2)最大值为
;(2)最大值为![]() ;(3)
;(3)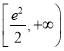 .
.
【解析】试题分析:(1)已知“![]() 在
在![]() 处与直线
处与直线![]() 相切”说明
相切”说明![]() ,
, ![]() ,联立可解得
,联立可解得![]() ;(2)要求最大值,首先通过导数研究函数
;(2)要求最大值,首先通过导数研究函数![]() 在
在![]() 上的单调性与极值,发现在此区间上只要一个极大值点,它一定是最大值点;(3)本小题不等式恒成立问题,有两个参数
上的单调性与极值,发现在此区间上只要一个极大值点,它一定是最大值点;(3)本小题不等式恒成立问题,有两个参数![]() ,因此要把问题进行转化,不等式
,因此要把问题进行转化,不等式![]() 对所有的
对所有的![]() ,
, ![]() 都成立,即
都成立,即![]() 对所有的
对所有的![]() ,
, ![]() 都成立,即
都成立,即![]() 对所有的
对所有的![]() ,
, ![]() 都成立,即
都成立,即![]() 对
对![]() 恒成立,即
恒成立,即![]() 对
对![]() 恒成立,
恒成立,
即a大于等于![]() 在区间
在区间![]() 上的最大值,下面只要求得于
上的最大值,下面只要求得于![]() 在区间
在区间![]() 上的最大值即可.
上的最大值即可.
试题解析:(1)![]() .
.
由函数![]() 在
在![]() 处与直线
处与直线![]() 相切,得
相切,得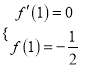 ,即
,即 .
.
解得: 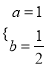 .
.
(2)由(1)得: ![]() ,定义域为
,定义域为![]() .
.
此时, ![]() ,令
,令![]() ,解得
,解得![]() ,令
,令![]() ,得
,得![]() .
.
所以![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上单调递减,
上单调递减,
所以![]() 在
在![]() 上的最大值为
上的最大值为![]() .
.
(3)若不等式![]() 对所有的
对所有的![]() ,
, ![]() 都成立,
都成立,
即![]() 对所有的
对所有的![]() ,
, ![]() 都成立,
都成立,
即![]() 对所有的
对所有的![]() ,
, ![]() 都成立,
都成立,
即![]() 对
对![]() 恒成立,
恒成立,
即![]() 对
对![]() 恒成立,
恒成立,
即a大于等于![]() 在区间
在区间![]() 上的最大值.
上的最大值.
令![]() ,则
,则![]() ,当
,当![]() 时,
时, ![]() ,
, ![]() 单调递增,
单调递增,
所以![]() ,
, ![]() 的最大值为
的最大值为![]() ,即
,即![]() .
.
所以a的取值范围为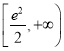 .
.


科目:高中数学 来源: 题型:
【题目】“微信运动”已成为当下热门的健身方式,小王的微信朋友圈内也有大量好友参与了“微信运动”,他随机选取了其中的40人(男、女各20人),记录了他们某一天的走路步数,并将数据整理如下:
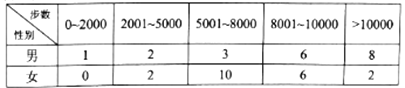
(1)若采用样本估计总体的方式,试估计小王的所有微信好友中每日走路步数超过5000步的概率;
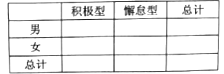
(2)已知某人一天的走路步数超过8000步被系统评定“积极型”,否则为“懈怠型”,根据题意完成下面的![]() 列联表,并据此判断能否有95%以上的把握认为“评定类型”与“性别”有关?
列联表,并据此判断能否有95%以上的把握认为“评定类型”与“性别”有关?
 附:
附: 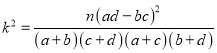 ,
,
| 0.10 | 0.05 | 0.025 | 0.010 |
| 2.706 | 3.841 | 5.024 | 6.635 |
查看答案和解析>>
科目:高中数学 来源: 题型:
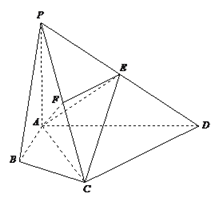
【题目】四棱锥P-ABCD中,∠ABC=∠ACD=90°,∠BAC=∠CAD=60°,PA⊥平面ABCD,
E为PD的中点,PA=2AB=2.
(1)若F为PC的中点,求证PC⊥平面AEF;
(2)求二面角![]() 的平面角的正弦值.
的平面角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某中学在高二年级开设大学选修课程《线性代数》,共有![]() 名同学选修,其中男同学
名同学选修,其中男同学![]() 名,女同学
名,女同学![]() 名.为了对这门课程的教学效果进行评估,学校按性别采取分层抽样的方法抽取
名.为了对这门课程的教学效果进行评估,学校按性别采取分层抽样的方法抽取![]() 人进行考核.
人进行考核.
(1)求抽取的![]() 人中男、女同学的人数;
人中男、女同学的人数;
(2)考核前,评估小组打算从选出的![]() 中随机选出
中随机选出![]() 名同学进行访谈,求选出的两名同学中恰有一名女同学的概率;
名同学进行访谈,求选出的两名同学中恰有一名女同学的概率;
(3)考核分答辩和笔试两项. ![]() 位同学的笔试成绩分别为
位同学的笔试成绩分别为![]() ;结合答辩情况,他们的考核成绩分别为
;结合答辩情况,他们的考核成绩分别为![]() .这
.这![]() 位同学笔试成绩与考核成绩的方差分别记为
位同学笔试成绩与考核成绩的方差分别记为![]() ,试比较
,试比较![]() 和
和![]() 的大小.(只需写出结论)
的大小.(只需写出结论)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给出下列四个命题:
①函数y=|x|与函数y= ![]() 表示同一个函数;
表示同一个函数;
②奇函数的图象一定通过直角坐标系的原点;
③函数y=3(x﹣1)2的图象可由y=3x2的图象向右平移1个单位得到;
④若函数f(x)的定义域为[0,2],则函数f(2x)的定义域为[0,4];
⑤设函数f(x)是在区间[a.b]上图象连续的函数,且f(a)f(b)<0,则方程f(x)=0在区间[a,b]上至少有一实根.
其中正确命题的序号是 . (填上所有正确命题的序号)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)=x3-3ax2+3bx的图像与直线12x+y-1=0相切于点(1,-11)。
(1)求a,b的值;
(2)讨论函数f(x)的单调性.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,M,N,K分别是正方体ABCD﹣A1B1C1D1的棱AB,CD,C1D1的中点. 
(1)求证:AN∥平面A1MK;
(2)求证:平面A1B1C⊥平面A1MK.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com