
【题目】已知平面向量 ![]() ,
, ![]() (
( ![]() ≠
≠ ![]() )满足
)满足 ![]() =2,且
=2,且 ![]() 与
与 ![]() ﹣
﹣ ![]() 的夹角为120° , t∈R,则|(1﹣t)
的夹角为120° , t∈R,则|(1﹣t) ![]() +t
+t ![]() |的最小值是 . 已知
|的最小值是 . 已知 ![]()
![]() =0,向量
=0,向量 ![]() 满足(
满足( ![]() ﹣
﹣ ![]() )(
)( ![]() ﹣
﹣ ![]() )=0,|
)=0,| ![]() ﹣
﹣ ![]() |=5,|
|=5,| ![]() ﹣
﹣ ![]() |=3,则
|=3,则 ![]()
![]() 的最大值为 .
的最大值为 .
【答案】![]() ;18
;18
【解析】解:①∵平面向量 ![]() 满足|
满足| ![]() |=2,且
|=2,且 ![]() 与
与 ![]() ﹣
﹣ ![]() 的夹角为120°,
的夹角为120°,
故当t( ![]() ﹣
﹣ ![]() )满足t|
)满足t| ![]() ﹣
﹣ ![]() |=
|= ![]() 时,|(1﹣t)
时,|(1﹣t) ![]() +t
+t ![]() |(t∈R)取最小值,
|(t∈R)取最小值,
此时由向量加法的三角形法则可得|(1﹣t) ![]() +
+ ![]() |(t∈R)的最小值是
|(t∈R)的最小值是 ![]() ;
;
②由 ![]()
![]() =0,建立如图所示的直角坐标系;
=0,建立如图所示的直角坐标系;
可设 ![]() =(m,0),
=(m,0), ![]() =(0,n),
=(0,n), ![]() =(x,y),
=(x,y),
∵| ![]() ﹣
﹣ ![]() |=5,
|=5,
∴m2+n2=25,记此圆为⊙M;
∵向量 ![]() 满足(
满足( ![]() ﹣
﹣ ![]() )(
)( ﹣
![]() )=0,
)=0,
∴x2+y2﹣mx﹣ny=0,
化为 ![]() +
+ ![]() =
= ![]() ,
,
说明点C在⊙M上;
∴| ![]() |=|
|=| ![]() ﹣
﹣ ![]() |=3,
|=3,
∴| ![]() |=|
|=| ![]() ﹣
﹣ ![]() |=4,
|=4,
过点C分别作CD⊥y轴,CE⊥x轴,垂足分别为D,E;
设∠CBD=θ,则∠OAC=θ,
则x=4sinθ=m﹣3cosθ,
∵ ![]()
![]() =mx=4sinθ(4sinθ+3cosθ)
=mx=4sinθ(4sinθ+3cosθ)
=16sin2θ+12sinθcosθ
=8(1﹣cos2θ)+6sin2θ
=10sin(2θ﹣φ)+8≤18;
∴ ![]()
![]() 的最大值为18.
的最大值为18.
所以答案是: ![]() ,18.
,18.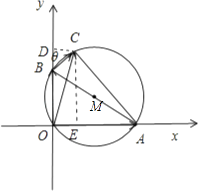


 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案科目:高中数学 来源: 题型:
【题目】是否存在过点(﹣5,﹣4)的直线l,使它与两坐标轴围成的三角形的面积为5?若存在,求出直线l的方程(化成直线方程的一般式);若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】△ABC的内角A,B,C的对边分别为a,b,c,已知△ABC的面积为![]()
(1)求sinBsinC;
(2)若6cosBcosC=1,a=3,求△ABC的周长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在直角坐标系中,已知曲线![]() 的参数方程为
的参数方程为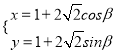 (
(![]() 为参数),在极坐标系中,直线
为参数),在极坐标系中,直线![]() 的方程为:
的方程为: ![]() ,直线
,直线![]() 的方程为
的方程为![]() .
.
(Ⅰ)写出曲线![]() 的直角坐标方程,并指出它是何种曲线;
的直角坐标方程,并指出它是何种曲线;
(Ⅱ)设![]() 与曲线
与曲线![]() 交于
交于![]() 两点,
两点, ![]() 与曲线
与曲线![]() 交于
交于![]() 两点,求四边形
两点,求四边形![]() 面积的取值范围.
面积的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知△ABC的内角A,B,C的对边分别为a,b,c,且b=acosc+ ![]() csinA.
csinA.
(1)求角A的大小;
(2)当a=3时,求△ABC周长的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱锥P-ABC中,PA⊥底面ABC, ![]() .点D,E,N分别为棱PA,PC,BC的中点,M是线段AD的中点,PA=AC=4,AB=2.
.点D,E,N分别为棱PA,PC,BC的中点,M是线段AD的中点,PA=AC=4,AB=2.
(Ⅰ)求证:MN∥平面BDE;
(Ⅱ)求二面角C-EM-N的正弦值;
(Ⅲ)已知点H在棱PA上,且直线NH与直线BE所成角的余弦值为![]() ,求线段AH的长.
,求线段AH的长.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,在平面直角坐标系xOy中,设椭圆E: ![]() =1(a>b>0),其中b=
=1(a>b>0),其中b= ![]() a,F为椭圆的右焦点,P(1,1)为椭圆E内一点,PF⊥x轴.
a,F为椭圆的右焦点,P(1,1)为椭圆E内一点,PF⊥x轴. 
(1)求椭圆E的方程;
(2)过P点作斜率为k1 , k2的两条直线分别与椭圆交于点A,C和B,D.若满足|AP||PC|=|BP||DP|,问k1+k2是否为定值?若是,请求出此定值;若不是,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设向量 ![]() =(4cosα,sinα),
=(4cosα,sinα), ![]() =(sinβ,4cosβ),
=(sinβ,4cosβ), ![]() =(cosβ,﹣4sinβ)
=(cosβ,﹣4sinβ)
(1)若 ![]() 与
与 ![]() ﹣2
﹣2 ![]() 垂直,求tan(α+β)的值;
垂直,求tan(α+β)的值;
(2)若β∈(﹣ ![]() ],求|
],求| ![]() |的取值范围.
|的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆经过点![]() ,点
,点![]() 是椭圆上在第一象限的点,直线
是椭圆上在第一象限的点,直线![]() 交
交![]() 轴于点
轴于点![]() ,直线
,直线![]() 交
交![]() 轴于点
轴于点![]() .
.
(Ⅰ)求椭圆的标准方程和离心率;
(Ⅱ)是否存在点![]() ,使得直线
,使得直线![]() 与直线
与直线![]() 平行?若存在,求出点
平行?若存在,求出点![]() 的坐标,若不存在,请说明理由.
的坐标,若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com