
【题目】已知函数 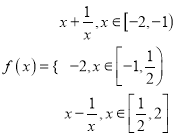 .
.
(1)求![]() 的值域;
的值域;
(2)设函数![]() ,
, ![]() ,若对于任意
,若对于任意![]() , 总存在
, 总存在![]() ,使得
,使得![]() 成立,求实数
成立,求实数![]() 的取值范围.
的取值范围.
【答案】(1) A = [-![]() ,-2]∪[-
,-2]∪[-![]() ,
, ![]() ];(2) (-,-
];(2) (-,-![]() ]∪[
]∪[![]() ,+).
,+).
【解析】试题分析:(1)先根据各段单调性确定各段值域,最后根据三者值域的并集得函数值域(2)由题意求![]() 值域包含
值域包含![]() 值域,再分别求对应值域,最后根据集合包含关系可得实数
值域,再分别求对应值域,最后根据集合包含关系可得实数![]() 关系式,解得取值范围.
关系式,解得取值范围.
试题解析: (1) 设![]() ,f (x1)-f (x2) = x1 +
,f (x1)-f (x2) = x1 +![]() -(x2 +
-(x2 +![]() ) = (x1-x2) (1-
) = (x1-x2) (1-![]() )
)
因为![]() ,
,
所以x1-x2 < 0, ![]() ,
, ![]() ,所以 1-
,所以 1-![]() > 0,
> 0,
所以 f (x1)-f (x2)< 0, f (x) 在 [-2,-1)是增函数.
同理可证f (x) 在 [![]() ,2] 也为增函数(略)
,2] 也为增函数(略)
∴ x [-2,-1) 时,f (x) [-![]() ,-2)
,-2)
x [![]() ,2] 时,f (x) [-
,2] 时,f (x) [-![]() ,
,![]() ]
]
∴ f (x) 的值域 A = [-![]() ,-2]∪[-
,-2]∪[-![]() ,
,![]() ]
]
(2) 设 g(x) 的值域为 B,则 B = [-2 | a |-2, 2 | a |-2]
依题意,A B
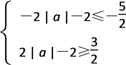
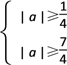 | a |≥
| a |≥![]()
∴ a 的取值范围是 (-,-![]() ]∪[
]∪[![]() ,+).
,+).


科目:高中数学 来源: 题型:
【题目】已知函数f(x)=ln(x+1)+ax2 , a>0.
(1)讨论函数f(x)的单调性;
(2)若函数f(x)在区间(﹣1,0)有唯一零点x0 , 证明: ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设命题p:实数x满足x2﹣4ax+3a2<0,其中a>0;命题q:实数x满足|x﹣3|≤1.
(1)若a=1,且p∧q为真,求实数x的取值范围;
(2)若¬p是¬q的充分不必要条件,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
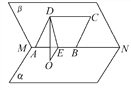
【题目】如图,已知二面角α-MN-β的大小为60°,菱形ABCD在平面β内,A,B两点在棱MN上,∠BAD=60°,E是AB的中点,DO⊥平面α,垂足为O.
(1)证明:AB⊥平面ODE.
(2)求异面直线BC与OD所成角的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知定义域为R的奇函数y=f(x)的导函数为y=f′(x),当x≠0时, ![]() >0,若a=f(1),b=﹣2f(﹣2),c=(ln
>0,若a=f(1),b=﹣2f(﹣2),c=(ln ![]() )f(ln
)f(ln ![]() ),则a,b,c的大小关系正确的是( )
),则a,b,c的大小关系正确的是( )
A.a<c<b
B.b<c<a
C.a<b<c
D.c<a<b
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知双曲线 ![]() ﹣
﹣ ![]() =1(a>0,b>0)的左、右焦点分别为F1、F2 , 点P(x0 ,
=1(a>0,b>0)的左、右焦点分别为F1、F2 , 点P(x0 , ![]() )为双曲线上一点,若△PF1F2的内切圆半径为1,且圆心G到原点O的距离为
)为双曲线上一点,若△PF1F2的内切圆半径为1,且圆心G到原点O的距离为 ![]() ,则双曲线的离心率是 .
,则双曲线的离心率是 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 的最小正周期为
的最小正周期为![]() ,且点
,且点![]() 是该函数图象的一个最高点.
是该函数图象的一个最高点.
(1)求函数![]() 的解析式;
的解析式;
(2)若![]() ,求函数
,求函数![]() 的值域;
的值域;
(3)把函数![]() 的图象向右平移
的图象向右平移![]() 个单位长度,得到函数
个单位长度,得到函数![]() 在
在![]() 上是单调增函数,求
上是单调增函数,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com