
【题目】已知![]() ,
,![]() 是
是![]() 轴正半轴上两点(
轴正半轴上两点(![]() 在
在![]() 的左侧),且
的左侧),且![]() ,过
,过![]() ,
,![]() 作
作![]() 轴的垂线,与抛物线
轴的垂线,与抛物线![]() 在第一象限分别交于
在第一象限分别交于![]() ,
,![]() 两点.
两点.
(Ⅰ)若![]() ,点
,点![]() 与抛物线
与抛物线![]() 的焦点重合,求直线
的焦点重合,求直线![]() 的斜率;
的斜率;
(Ⅱ)若![]() 为坐标原点,记
为坐标原点,记![]() 的面积为
的面积为![]() ,梯形
,梯形![]() 的面积为
的面积为![]() ,求
,求![]() 的取值范围.
的取值范围.
科目:高中数学 来源: 题型:
【题目】某商场举行优惠促销活动,顾客仅可以从以下两种优惠方案中选择一种.
方案一:每满100元减20元;
方案二:满100元可抽奖一次.具体规则是从装有2个红球、2个白球的箱子随机取出3个球(逐个有放回地抽取),所得结果和享受的优惠如下表:(注:所有小球仅颜色有区别)
红球个数 | 3 | 2 | 1 | 0 |
实际付款 | 7折 | 8折 | 9折 | 原价 |
(1)该商场某顾客购物金额超过100元,若该顾客选择方案二,求该顾客获得7折或8折优惠的概率;
(2)若某顾客购物金额为180元,选择哪种方案更划算?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,某旅游区拟建一主题游乐园,该游乐区为五边形区域ABCDE,其中三角形区域ABE为主题游乐区,四边形区域为BCDE为休闲游乐区,AB、BC,CD,DE,EA,BE为游乐园的主要道路(不考虑宽度).![]()
![]() .
.

(I)求道路BE的长度;
(Ⅱ)求道路AB,AE长度之和的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
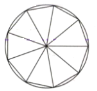
【题目】刘徽(约公元225年-295年),魏晋期间伟大的数学家,中国古典数学理论的奠基人之一他在割圆术中提出的,“割之弥细,所失弥少,割之又割,以至于不可割,则与圆周合体而无所失矣”,这可视为中国古代极限观念的佳作,割圆术的核心思想是将一个圆的内接正n边形等分成n个等腰三角形(如图所示),当n变得很大时,这n个等腰三角形的面积之和近似等于圆的面积,运用割圆术的思想,得到![]() 的近似值为( )
的近似值为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
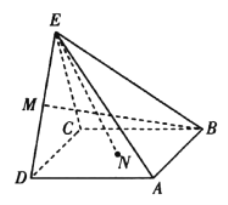
【题目】如图所示,在四棱锥![]() 中,底面
中,底面![]() 是边长为
是边长为![]() 的正方形,
的正方形,![]() 是正三角形,
是正三角形,![]() 为线段
为线段![]() 的中点,点
的中点,点![]() 为底面
为底面![]() 内的动点,则下列结论正确的是( )
内的动点,则下列结论正确的是( )
A.若![]() 时,平面
时,平面![]() 平面
平面![]()
B.若![]() 时,直线
时,直线![]() 与平面
与平面![]() 所成的角的正弦值为
所成的角的正弦值为![]()
C.若直线![]() 和
和![]() 异面时,点
异面时,点![]() 不可能为底面
不可能为底面![]() 的中心
的中心
D.若平面![]() 平面
平面![]() ,且点
,且点![]() 为底面
为底面![]() 的中心时,
的中心时,![]()
![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() ,不与坐标轴垂直的直线
,不与坐标轴垂直的直线![]() 与抛物线交于
与抛物线交于![]() 两点,当
两点,当![]() 且
且![]() 时,
时,![]() .
.
(1)求抛物线的标准方程;
(2)若![]() 过定点
过定点![]() ,点
,点![]() 关于
关于![]() 轴的对称点为
轴的对称点为![]() ,证明:直线
,证明:直线![]() 过定点,并求出定点坐标.
过定点,并求出定点坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com