
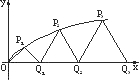
 如图,设P1,P2,P3,…,Pn,…是曲线y=
如图,设P1,P2,P3,…,Pn,…是曲线y=| x |
| 1 |
| 3 |
| 1 |
| 3 |
| ||
| 3 |
| 2 |
| 3 |
| 1 |
| 3 |
| 2 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
| 3 |
| 1 |
| 3 |
| 3 |
| x |
| 1 |
| 3 |
| ||
| 3 |
| 2 |
| 3 |
| 1 |
| 3 |
| 2 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
| 3 |
| 1 |
| 3 |
| x |
| (k+1)2 |
| 3 |
| ||
| 3 |
| ||
| 3 |
| 2 | ||
|
| 2 |
| 3 |
| 1 |
| 3 |
| 2 |
| 3 |
| 1 |
| 3 |


 中考解读考点精练系列答案
中考解读考点精练系列答案 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案科目:高中数学 来源:学习周报 数学 人教课标高二版(A选修1-2) 2009-2010学年 第39期 总第195期 人教课标版(A选修1-2) 题型:022
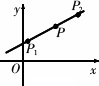
线与角是几何中两种基本的量,因而可以取线段的类比源.如图,设P1(x1,y1),P2(x2,y2),如果点P(x,y)分线段P1P2之比为λ=![]() ,则由定比分点坐标公式可得点P的坐标为x=
,则由定比分点坐标公式可得点P的坐标为x=![]() ,y=
,y=![]() .
.
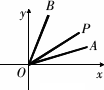
在下图中,设∠xOA=α,∠xOB=β,若λ=![]() ,则有类比猜想∠xOP=________.
,则有类比猜想∠xOP=________.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
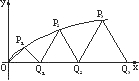 如图,设P1,P2,P3,…,Pn,…是曲线y=
如图,设P1,P2,P3,…,Pn,…是曲线y= 上的点列,Q1,Q2,Q3,…,Qn,…是x轴正半轴上的点列,且△OQ1P1,△Q1Q2P2,…,△Qn-1QnPn,…都是正三角形,设它们的边长为a1,a2,…,an,…,求证:a1+a2+…+an=
上的点列,Q1,Q2,Q3,…,Qn,…是x轴正半轴上的点列,且△OQ1P1,△Q1Q2P2,…,△Qn-1QnPn,…都是正三角形,设它们的边长为a1,a2,…,an,…,求证:a1+a2+…+an= n(n+1).
n(n+1).查看答案和解析>>
科目:高中数学 来源: 题型:
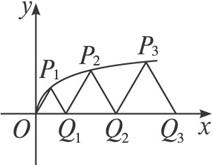
图1
查看答案和解析>>
科目:高中数学 来源:2006年高考第一轮复习数学:13.1 数学归纳法(解析版) 题型:解答题
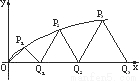 如图,设P1,P2,P3,…,Pn,…是曲线y=
如图,设P1,P2,P3,…,Pn,…是曲线y=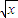 上的点列,Q1,Q2,Q3,…,Qn,…是x轴正半轴上的点列,且△OQ1P1,△Q1Q2P2,…,△Qn-1QnPn,…都是正三角形,设它们的边长为a1,a2,…,an,…,求证:a1+a2+…+an=
上的点列,Q1,Q2,Q3,…,Qn,…是x轴正半轴上的点列,且△OQ1P1,△Q1Q2P2,…,△Qn-1QnPn,…都是正三角形,设它们的边长为a1,a2,…,an,…,求证:a1+a2+…+an= n(n+1).
n(n+1).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com