
 ij������Ϊ��ȷ��һ����Ϊ�����ľ����õ�����������˽�ȫ�о����ճ��õ����ķֲ�������ֲ��ó�������ķ�ʽ�������nλ������2012����¾��õ�������λ���ȣ����ݣ�����ͳ�ƽ������ͼ����
ij������Ϊ��ȷ��һ����Ϊ�����ľ����õ�����������˽�ȫ�о����ճ��õ����ķֲ�������ֲ��ó�������ķ�ʽ�������nλ������2012����¾��õ�������λ���ȣ����ݣ�����ͳ�ƽ������ͼ����| �� �� | Ƶ �� | Ƶ �� |
| [0��10�� | 0.05 | |
| [10��20�� | 0.10 | |
| [20��30�� | 30 | |
| [30��40�� | 0.25 | |
| [40��50�� | 0.15 | |
| [50��60] | 15 | |
| �� �� | n | 1 |
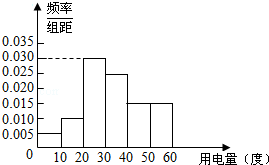
���� ��1������Ƶ�ʷֲ�ֱ��ͼ�����¾��õ�������λ����ƽ��������ֵ��
��2�������n����ȡ��8λ�������¾��õ�����30��40�ȵľ����������������������1λ�����¾��õ�����30��40�ȵĸ��ʣ�
��3��X���Ӷ���ֲ����������¾��õ�����30��40�ȵľ�����X�ķֲ��У�
��� �⣺��1����λ������ֵΪ32��
ƽ��������ֵΪ0.05��5+0.1��15+0.3��25+0.25��35+0.15��45+0.15��55=33����4�֣�
��2����$\frac{30}{n}=0.3$��n=100��
��ȡ��8λ�������¾��õ�����30��40�ȵľ�����$25��\frac{8}{100}=2$�ˣ�
������1λ�����¾��õ�����30��40�ȸ���Ϊ$1-\frac{C_6^2}{C_8^2}=\frac{13}{28}$����8�֣�
��3����ȡ1λ�����¾��õ��� ��30��40�ȵĸ���Ϊ$\frac{25}{100}=\frac{1}{4}$��
��$X��B��3��\frac{1}{4}��$
��X�ķֲ���Ϊ
| x | 0 | 1 | 2 | 3 |
| P | $\frac{27}{64}$ | $\frac{27}{64}$ | $\frac{9}{64}$ | $\frac{1}{64}$ |
���� ���⿼��Ƶ�ʷֲ�ֱ��ͼ��������ʵ���⣬������ɢ����������ķֲ�������ѧ������ȷ��������ȡֵ�������Ӧ�ĸ����ǹؼ���



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 177 | B�� | 157 | C�� | 417 | D�� | 367 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\sqrt{2}$ | B�� | $\sqrt{3}$ | C�� | $\sqrt{6}$ | D�� | $2\sqrt{2}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com