
【题目】已知实数![]() ,设函数
,设函数![]()
(1)当![]() 时,求函数
时,求函数![]() 的单调区间;
的单调区间;
(2)对任意![]() 均有
均有![]() 求
求![]() 的取值范围.
的取值范围.
注:![]() 为自然对数的底数.
为自然对数的底数.
【答案】(1)![]() 的单调递增区间是
的单调递增区间是![]() ,单调递减区间是
,单调递减区间是![]() ;(2)
;(2)![]() .
.
【解析】
(1)首先求得导函数的解析式,然后结合函数的解析式确定函数的单调区间即可.
(2)由题意首先由函数在特殊点的函数值得到a的取值范围,然后证明所得的范围满足题意即可.
(1)当![]() 时,
时,![]() ,函数的定义域为
,函数的定义域为![]() ,且:
,且:
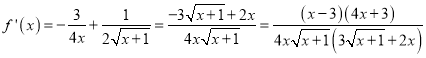 ,
,
因此函数![]() 的单调递增区间是
的单调递增区间是![]() ,单调递减区间是
,单调递减区间是![]() .
.
(2)构造函数![]() ,
,
注意到:![]() ,
,
注意到![]() 时
时![]() 恒成立,满足
恒成立,满足![]() ;
;
当![]() 时,
时,![]() ,不合题意,
,不合题意,
且![]() ,解得:
,解得:![]() ,故
,故![]() .
.
下面证明![]() 刚好是满足题意的实数a的取值范围.
刚好是满足题意的实数a的取值范围.
分类讨论:
(a)当![]() 时,
时,![]() ,
,
令![]() ,则:
,则:
![]()
![]()

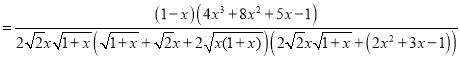 ,
,
易知![]() ,则函数
,则函数![]() 单调递减,
单调递减,![]() ,满足题意.
,满足题意.
(b)当![]() 时,
时,![]() 等价于
等价于![]() ,
,
左侧是关于a的开口向下的二次函数![]() ,
,
其判别式![]() ,
,
令![]() ,注意到当
,注意到当![]() 时,
时,![]() ,
,
于是![]() 在
在![]() 上单调递增,而
上单调递增,而![]() ,
,
于是当![]() 时命题成立,
时命题成立,
而当![]() 时,此时
时,此时![]() 的对称轴为
的对称轴为![]() 随着
随着![]() 递增,
递增,
于是对称轴在![]() 的右侧,而
的右侧,而![]() 成立,(不等式等价于
成立,(不等式等价于![]() ).
).
因此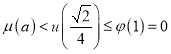 .
.
综上可得:实数a的取值范围是![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】已知![]() ,直线
,直线![]() 分别交
分别交![]() 轴、
轴、![]() 轴的正半轴于
轴的正半轴于![]() 、
、![]() 两点,
两点,![]() 为坐标原点.
为坐标原点.
(1)若直线![]() 方程为
方程为![]() (
(![]() ),且
),且![]() ,求
,求![]() 的值;
的值;
(2)若直线![]() 经过点
经过点![]() ,设
,设![]() 的斜率为
的斜率为![]() ,
,![]() 为线段
为线段![]() 的中点,求
的中点,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知不共线向量![]() ,
,![]() 满足|
满足|![]() |=3,|
|=3,|![]() |=2,(2
|=2,(2![]() 3
3![]() )(2
)(2![]() )=20.
)=20.
(1)求![]()
![]() ;
;
(2)是否存在实数λ,使λ![]() 与
与![]() 2
2![]() 共线?
共线?
(3)若(k![]() 2
2![]() )⊥(
)⊥(![]() ),求实数k的值.
),求实数k的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
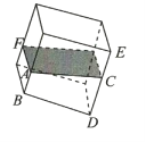
【题目】在一个长方体的容器中,里面装有少量的水,现在将容器绕着其底部的一条棱倾斜.
(1)在倾斜的过程中,水面的形状不断变化,可能是矩形,也可能变成不是矩形的平行四边形,对吗?
(2)在倾斜的过程中,水的形状也不断变化,可以是棱柱,也可能变为棱台或棱锥,对吗?
(3)如果倾斜时,不是绕着底部的一条棱,而是绕着其底面的一个顶点,上面的第(1)问和第(2)问对不对?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知动点P与两个定点O(0,0),A(3,0)的距离的比值为2,点P的轨迹为曲线C.
(1)求曲线C的轨迹方程
(2)过点(﹣1,0)作直线与曲线C交于A,B两点,设点M坐标为(4,0),求△ABM面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图1,在△![]() 中,
中,![]() ,
,![]() 分别为
分别为![]() ,
,![]() 的中点,
的中点,![]() 为
为![]() 的中点,
的中点, ![]() ,
,![]() .将△
.将△![]() 沿
沿![]() 折起到△
折起到△![]() 的位置,使得平面
的位置,使得平面![]() 平面
平面![]() ,
, ![]() 为
为![]() 的中点,如图2.
的中点,如图2.
(Ⅰ)求证: ![]() 平面
平面![]() ;
;
(Ⅱ)求F到平面A1OB的距离.

图1 图2
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com