
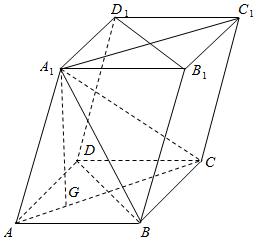
 如图,在斜四棱柱ABCD-A1B1C1D1的底面是边长为2$\sqrt{3}$的菱形,且∠BAD=$\frac{π}{3}$,若∠AA1C=$\frac{π}{2}$,且A1在底面ABCD上的射影为△ABD的重心G.
如图,在斜四棱柱ABCD-A1B1C1D1的底面是边长为2$\sqrt{3}$的菱形,且∠BAD=$\frac{π}{3}$,若∠AA1C=$\frac{π}{2}$,且A1在底面ABCD上的射影为△ABD的重心G.分析 (1)设AC,BD交点为O,则O在AC上,由A1G⊥平面ABCD得A1G⊥BD,由菱形性质得AC⊥BD,故而BD⊥平面ACC1A1,于是平面ACC1A1⊥平面BDD1B1;
(2)利用等体积转换,求三棱锥C1-A1BC的体积.
解答 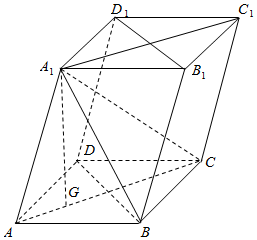 (1)证明:连结AC、BD相交于O
(1)证明:连结AC、BD相交于O
∵四边形ABCD为菱形,且$∠BAD=\frac{π}{3}$,∴△ABD为等边三角形,
∵A1在底面ABCD上的射影G为△ABD的重心,∴G∈ACA1G⊥平面ABCD,∴BD⊥A1G,
又四边形ABCD为菱形,∴BD⊥AC,
∵A1G与AC相交于G,∴BD⊥平面ACC1A1.
又BD在平面BDD1B1内,∴平面ACC1A1⊥平面BDD1B1.
(2)解:∵$AG=\frac{{\sqrt{3}}}{2}•2\sqrt{3}×\frac{2}{3}=2,GC=4$,
∴在Rt△AA1C中,由射影定理知${A_1}{G^2}=AG•GC$,求得${A_1}G=2\sqrt{2},AO=3$.${V_{{C_1}-{A_1}BC}}={V_{{B_1}-{A_1}BC}}={V_{A-{A_1}BC}}={V_{{A_1}-ABC}}$,且△ABC是腰长为$2\sqrt{3}$,顶角为$\frac{2π}{3}$的等腰三角形,
∴${V_{A-ABC}}=\frac{1}{3}×2\sqrt{2}×({\frac{{\sqrt{3}}}{4}×12})=2\sqrt{6}$,即三棱锥C1-A1BC的体积$2\sqrt{6}$.
点评 本题考查了面面垂直的判定,三棱锥C1-A1BC的体积的计算,考查学生分析解决问题的能力,属于中档题.


科目:高中数学 来源:2015-2016学年江苏泰兴中学高二上学期期末数学(文)试卷(解析版) 题型:填空题
在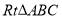 中,
中,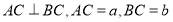 ,则
,则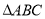 的外接圆半径
的外接圆半径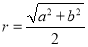 ;类比到空间,若三棱锥
;类比到空间,若三棱锥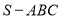 的三条侧棱
的三条侧棱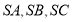 两两互相垂直,且长度分别为
两两互相垂直,且长度分别为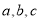 ,则三棱锥
,则三棱锥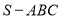 的外接球的半径
的外接球的半径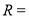 .
.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
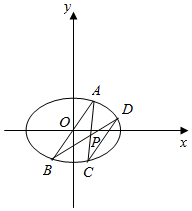 如图,在平面直角坐标系xOy中,已知椭圆E:$\frac{x^2}{a^2}$+$\frac{y^2}{b^2}$=1(a>b>0)的离心率为$\frac{{\sqrt{2}}}{2}$,点A(${\frac{1}{3}$,$\frac{2}{3}}$)在椭圆E上,射线AO与椭圆E的另一交点为B,点P(-4t,t)在椭圆E内部,射线AP,BP与椭圆E的另一交点分别为C,D.
如图,在平面直角坐标系xOy中,已知椭圆E:$\frac{x^2}{a^2}$+$\frac{y^2}{b^2}$=1(a>b>0)的离心率为$\frac{{\sqrt{2}}}{2}$,点A(${\frac{1}{3}$,$\frac{2}{3}}$)在椭圆E上,射线AO与椭圆E的另一交点为B,点P(-4t,t)在椭圆E内部,射线AP,BP与椭圆E的另一交点分别为C,D.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
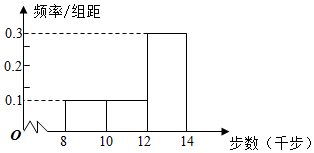 王师傅为响应国家开展全民健身运动的号召,每天坚持“健步走”,并用计步器对每天的“健步走”步数进行统计,他从某个月中随机抽取10天“健步走”的步数,绘制出的频率分布直方图如图所示.
王师傅为响应国家开展全民健身运动的号召,每天坚持“健步走”,并用计步器对每天的“健步走”步数进行统计,他从某个月中随机抽取10天“健步走”的步数,绘制出的频率分布直方图如图所示.| 每天的步数分组 (千步) | [8,10) | [10,12) | [12,14] |
| 评价级别 | 及格 | 良好 | 优秀 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com