
【题目】已知0<a<1,f(x)=ax , g(x)=logax,h(x)= ![]() ,当x>1时,则有( )
,当x>1时,则有( )
A.f(x)<g(x)<h(x)
B.g(x)<f(x)<h(x)
C.g(x)<h(x)<f(x)
D.h(x)<g(x)<f(x)
【答案】B
【解析】解:∵0<a<1,∴f(x)=ax在R上单调递减,
∴当x>1时,f(x)<f(1)=a<1,
结合指数函数的值域可得f(x)∈(0,1);
同理∵0<a<1,∴g(x)=logax在(0,+∞)上单调递减,
∴当x>1时,g(x)<g(1)=0,
结合对数函数的值域可得g(x)∈(﹣∞,0);
又∴h(x)= ![]() 在[0,+∞)上单调递增,
在[0,+∞)上单调递增,
∴当x>1时,g(x)>h(1)=1,
故g(x)<f(x)<h(x),
故选:B.
【考点精析】通过灵活运用指数函数的图像与性质,掌握a0=1, 即x=0时,y=1,图象都经过(0,1)点;ax=a,即x=1时,y等于底数a;在0<a<1时:x<0时,ax>1,x>0时,0<ax<1;在a>1时:x<0时,0<ax<1,x>0时,ax>1即可以解答此题.


科目:高中数学 来源: 题型:
【题目】如图,直线![]() 与抛物线
与抛物线![]() 交于A、B两点,线段AB的垂直平分线与直线y=-5交于Q点.
交于A、B两点,线段AB的垂直平分线与直线y=-5交于Q点.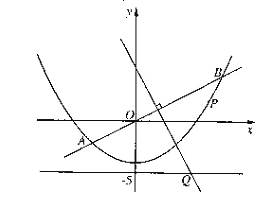
(1)求点Q的坐标;
(2)当P为抛物线上位于线段AB下方(含A、B)的动点时,求ΔOPQ面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,正方体ABCD﹣A′B′C′D′中,E是棱BC的中点,G是棱DD′的中点,则异面直线GB与B′E所成的角为( ) 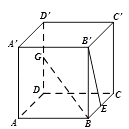
A.120°
B.90°
C.60°
D.30°
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=a( ![]() )x+bx2+cx(α∈R,b≠0,c∈R),若{x|f(x)=0}={x|f(f(x))=0}≠,则实数c的取值范围为( )
)x+bx2+cx(α∈R,b≠0,c∈R),若{x|f(x)=0}={x|f(f(x))=0}≠,则实数c的取值范围为( )
A.(0,4)
B.[0,4]
C.(0,4]
D.[0,4)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=cos(ωx+φ)(ω>0,﹣π<φ<0)的最小正周期为π,且它的图象过点( ![]() ,
, ![]() ).
).
(1)求ω,φ的值;
(2)求函数y=f(x)的单调增区间.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了解某高级中学学生的体重状况,打算抽取一个容量为n的样本,已知该校高一、高二、高三学生的数量之比依次为4:3:2,现用分层抽样的方法抽出的样本中高三学生有10人,那么样本容量n为( )
A.50
B.45
C.40
D.20
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知向量 ![]() =(2cosx,
=(2cosx, ![]() sinx),
sinx), ![]() =(3cosx,﹣2cosx),设函数f(x)=
=(3cosx,﹣2cosx),设函数f(x)= ![]()
![]()
(1)求f(x)的最小正周期;
(2)若x∈[0, ![]() ],求f(x)的值域.
],求f(x)的值域.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com