
【题目】已知椭圆C: ![]() (a>b>0)经过点(2,
(a>b>0)经过点(2, ![]() )且离心率等于
)且离心率等于 ![]() ,点A,B分别为椭圆C的左右顶点,点P在椭圆C上.
,点A,B分别为椭圆C的左右顶点,点P在椭圆C上.
(1)求椭圆C的方程;
(2)M,N是椭圆C上非顶点的两点,满足OM∥AP,ON∥BP,求证:三角形MON的面积是定值.
【答案】
(1)解:椭圆C: ![]() (a>b>0)经过点(2,
(a>b>0)经过点(2, ![]() )且离心率等于
)且离心率等于 ![]() ,
,
可得 ![]() =
= ![]() ,即:
,即: ![]() ,
, ![]() ,解得a2=8,b2=4,
,解得a2=8,b2=4,
所求椭圆方程为: ![]()
(2)证明:由题意M,N是椭圆C上非顶点的两点,
且AP∥OM,BP∥ON,设P(2 ![]() cosθ,2sinθ)
cosθ,2sinθ)
则直线AP,BP斜率必存在且不为0,
又由已知kAPkBP= ![]() =
= ![]() =-
=- ![]() .
.
因为AP∥OM,BP∥ON,所以kOMkON=- ![]()
设直线MN的方程为x=my+t,代入椭圆方程 ![]() ,
,
得(2+m2)y2+2mty+t2﹣8=0…①,
设M,N的坐标分别为M(x1,y1),N(x2,y2),
则y1+y2=﹣ ![]() ,y1y2=
,y1y2= ![]() ,x1x2=
,x1x2=
m2y1y2+mt(y1+y2)+t2= ![]() ,
,
所以kOMkON= ![]() =
= ![]() =﹣
=﹣ ![]() ,得t2=2m2+4,
,得t2=2m2+4,
又S△MON= ![]() |t||y1﹣y2|=
|t||y1﹣y2|= ![]() =
= ![]() =
= 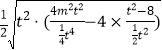 =
= ![]() =2
=2 ![]() ,
,
即△MON的面积为定值2 ![]()
【解析】(1)利用椭圆的离心率以及椭圆结果的点,求出长半轴与短半轴的长,即可得到椭圆方程;(2)求出kAPkBP=﹣ ![]() ,设直线MN的方程为x=my+t,代入椭圆方程,利用kOMkON=﹣
,设直线MN的方程为x=my+t,代入椭圆方程,利用kOMkON=﹣ ![]() ,推出t2=2m2+4,利用三角形的面积公式,化简求解即可推出结论.
,推出t2=2m2+4,利用三角形的面积公式,化简求解即可推出结论.
【考点精析】掌握椭圆的标准方程是解答本题的根本,需要知道椭圆标准方程焦点在x轴:![]() ,焦点在y轴:
,焦点在y轴:![]() .
.


科目:高中数学 来源: 题型:
【题目】过双曲线 ![]() =1(a,b>0)的右焦点F作一条渐近线的垂线,垂足为P,线段OP的垂直平分线交y轴于点Q(其中O为坐标原点).若△OFP的面积是△OPQ的面积的4倍,则该双曲线的离心率为( )
=1(a,b>0)的右焦点F作一条渐近线的垂线,垂足为P,线段OP的垂直平分线交y轴于点Q(其中O为坐标原点).若△OFP的面积是△OPQ的面积的4倍,则该双曲线的离心率为( )
A.![]()
B.![]()
C.2
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若定义域为R的偶函数y=f(x)满足f(x+2)+f(x)=0,且当x∈[0,2]时,f(x)=2﹣x2 , 则方程f(x)=2sinx在[﹣3π,3π]内根的个数是 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=|lg(x﹣1)|,若1<a<b且f(a)=f(b),则a+2b的取值范围为( )
A.![]()
B.![]()
C.(6,+∞)
D.[6,+∞)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆C的方程为(x﹣3)2+y2=1,圆M的方程为(x﹣3﹣3cosθ)2+(y﹣3sinθ)2=1(θ∈R),过M上任意一点P作圆C的两条切线PA,PB,切点分别为A、B,则∠APB的最大值为 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知曲线C在直角坐标系xOy下的参数方程为 ![]() (θ为参数).以O为极点,x轴的非负半轴为极轴建立极坐标系.
(θ为参数).以O为极点,x轴的非负半轴为极轴建立极坐标系.
(1)求曲线C的极坐标方程;
(2)直线l的极坐标方程是ρcos(θ﹣ ![]() )=3
)=3 ![]() ,射线OT:θ=
,射线OT:θ= ![]() (ρ>0)与曲线C交于A点,与直线l交于B,求线段AB的长.
(ρ>0)与曲线C交于A点,与直线l交于B,求线段AB的长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲抛掷均匀硬币2017次,乙抛掷均匀硬币2016次,下列四个随机事件的概率是0.5的是( )
①甲抛出正面次数比乙抛出正面次数多;
②甲抛出反面次数比乙抛出正面次数少;
③甲抛出反面次数比甲抛出正面次数多;
④乙抛出正面次数与乙抛出反面次数一样多.
A.①②
B.①③
C.②③
D.②④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)= 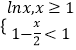 ,若F(x)=f[f(x)+1]+m有两个零点x1 , x2 , 则x1+x2的取值范围是( )
,若F(x)=f[f(x)+1]+m有两个零点x1 , x2 , 则x1+x2的取值范围是( )
A.[4﹣2ln2,+∞)
B.[1+ ![]() ,+∞)
,+∞)
C.[4﹣2ln2,1+ ![]() )
)
D.[﹣∞,1+ ![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,三棱柱ABC﹣A1B1C1中,底面是边长为2的正三角形,侧棱AA1⊥底面ABC,D为AB的中点,且A1D与底面ABC所成角的正切值为2,则三棱锥A1﹣ACD外接球的表面积为 . 
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com