考点:用空间向量求平面间的夹角,异面直线及其所成的角
专题:计算题,空间位置关系与距离,空间角
分析:(I)由线面垂直的性质和判定,即可得到AA
1⊥平面ABC,AB⊥AC,以A为坐标原点,AC,AB,AA
1所在直线为x,y,z轴,建立空间直角坐标系,求出A
1(0,0,4),B(0,3,0),C
1(4,0,4),则
=(4,0,4),
=(0,3,-4),再由向量的夹角公式即可得到所求值;
(II)通过(Ⅰ)建立的空间直角坐标系,设出所求的两个平面的法向量,运用向量垂直的条件:数量积为0,再利用两个平面的法向量的夹角即可得到二面角.
解答:
解:(I)∵AA
1C
1C是正方形,∴AA
1⊥AC
又∵AB⊥平面AA
1C
1C,AB⊥AC,AB⊥AA
1,
∴AA
1⊥平面ABC,由AC=4,AB=3,得BC=5,
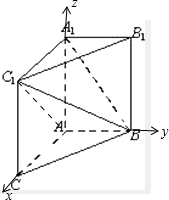
以A为坐标原点,AC,AB,AA
1所在直线为x,y,z轴,
建立如图所示的空间直角坐标系,则A
1(0,0,4),B(0,3,0),
C
1(4,0,4),则
=(4,0,4),
=(0,3,-4),
cos<
,>=
=
=-
.
故直线A C
1与直线A
1B夹角的余弦值为
;
(Ⅱ)由(Ⅰ)得A
1(0,0,4),B(0,3,0),B
1(0,3,4),
C
1(4,0,4),∴
=(0,-3,4),
=(4,-3,4),
=(0,0,4),
设平面A
1BC
1的法向量为
=(x
1,y
1,z
1),
平面B
1BC
1的法向量为
=(x
2,y
2,z
2).
则
| | •=4x1-3y1+4z1=0 | | •=-3y1+4z1=0 |
| |
,
令y
1=4,解得x
1=0,z
1=3,∴
=(0,4,3),
,
令x
2=3,解得y
2=4,z
2=0,∴
=(3,4,0).
cos<
,>=
=
=
.
∴二面角A
1-BC
1-B
1的余弦值为
.
点评:本题综合考查了线面垂直的判定与性质定理、面面垂直的性质定理、通过建立空间直角坐标系利用法向量求二面角的方法、向量垂直与数量积得关系等基础知识与基本方法,考查了空间想象能力、推理能力和计算能力.

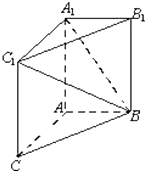 如图,在三棱柱ABC-A1B1C1中,AA1C1C是边长为4的正方形,AB⊥平面AA1C1C,AB=3.
如图,在三棱柱ABC-A1B1C1中,AA1C1C是边长为4的正方形,AB⊥平面AA1C1C,AB=3. 解:(I)∵AA1C1C是正方形,∴AA1⊥AC
解:(I)∵AA1C1C是正方形,∴AA1⊥AC

 提分百分百检测卷系列答案
提分百分百检测卷系列答案 宝贝计划期末冲刺夺100分系列答案
宝贝计划期末冲刺夺100分系列答案 能考试全能100分系列答案
能考试全能100分系列答案