
【题目】已知函数![]() 在x=-1与x=2处都取得极值.
在x=-1与x=2处都取得极值.
(1)求![]() 的值及函数
的值及函数![]() 的单调区间;
的单调区间;
(2)若对![]() ,不等式
,不等式![]() 恒成立,求c的取值范围.
恒成立,求c的取值范围.
【答案】(1)见解析;(2)![]()
【解析】
(1)函数在极值点的导数为零,利用![]() 求
求![]() ,再利用导数的正负求其单调区间(2)利用函数单调性,分析
,再利用导数的正负求其单调区间(2)利用函数单调性,分析![]() 的最大值,只需
的最大值,只需![]() 即可.
即可.
(1)f′(x)=3x2+2ax+b,由题意得
![]() 即
即![]() 解得
解得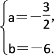
∴f(x)=x3-![]() x2-6x+c,f′(x)=3x2-3x-6.
x2-6x+c,f′(x)=3x2-3x-6.
令f′(x)<0,解得-1<x<2;
令f′(x)>0,解得x<-1或x>2.
∴f(x)的减区间为(-1,2),
增区间为(-∞,-1),(2,+∞).
(2)由(1)知,f(x)在(-∞,-1)上单调递增;在(-1,2)上单调递减;在(2,+∞)上单调递增.
∴x∈时,f(x)的最大值即为:f(-1)与f(3)中的较大者.
f(-1)=![]() +c,f(3)=-
+c,f(3)=-![]() +c.
+c.
∴当x=-1时,f(x)取得最大值.
要使f(x)+![]() c<c2,只需c2>f(-1)+
c<c2,只需c2>f(-1)+![]() c,即2c2>7+5c,解得c<-1或c>
c,即2c2>7+5c,解得c<-1或c>![]() .
.
∴c的取值范围为(-∞,-1)∪![]() .
.


 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案科目:高中数学 来源: 题型:
【题目】已知圆![]() 过点
过点![]() ,且圆心
,且圆心![]() 在直线
在直线![]() 上,过点
上,过点![]() 的直线交圆
的直线交圆![]() 于
于![]() 两点,过点
两点,过点![]() 分别做圆
分别做圆![]() 的切线,记为
的切线,记为![]() .
.
(Ⅰ)求圆![]() 的方程;
的方程;
(Ⅱ)求证:直线![]() 的交点都在同一条直线上,并求出这条直线的方程.
的交点都在同一条直线上,并求出这条直线的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在对人们的休闲方式的一次调查中,共调查了124人,其中女性70人,男性54人.女性中有43人主要的休闲方式是看电视,另外27人主要的休闲方式是运动;男性中有21人主要的休闲方式是看电视,另外33人主要的休闲方式是运动.
(1)根据以上数据建立一个2×2的列联表;
(2)根据所给的独立检验临界值表,你最多能有多少把握认为性别与休闲方式有关系?附:独立检验临界值表
P(K2≥k0) | 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
k0 | 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在心理学研究中,常采用对比试验的方法评价不同心理暗示对人的影响,具体方法如下:将参加试验的志愿者随机分成两组,一组接受甲种心理暗示,另一组接受乙种心理暗示,通过对比这两组志愿者接受心理暗示后的结果来评价两种心理暗示的作用,现有6名男志愿者A1 , A2 , A3 , A4 , A5 , A6和4名女志愿者B1 , B2 , B3 , B4 , 从中随机抽取5人接受甲种心理暗示,另5人接受乙种心理暗示.(12分)
(Ⅰ)求接受甲种心理暗示的志愿者中包含A1但不包含B1的概率.
(Ⅱ)用X表示接受乙种心理暗示的女志愿者人数,求X的分布列与数学期望EX.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若函数f(x)=kax﹣a﹣x(a>0且a≠1)在(﹣∞,+∞)上既是奇函数又是增函数,则函数g(x)=loga(x+k)的图象是( )
A.
B.
C.
D.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知向量 ![]() =(sin(x+
=(sin(x+ ![]() ),1),
),1), ![]() =(4,4cosx﹣
=(4,4cosx﹣ ![]() )
)
(1)若 ![]() ⊥
⊥ ![]() ,求sin(x+
,求sin(x+ ![]() )的值;
)的值;
(2)设f(x)= ![]()
![]() ,若α∈[0,
,若α∈[0, ![]() ],f(α﹣
],f(α﹣ ![]() )=2
)=2 ![]() ,求cosα的值.
,求cosα的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知某书店共有韩寒的图书6种,其中价格为25元的有2种,18元的有3种,16元的有1种.书店若把这6种韩寒的图书打包出售,据统计每套的售价与每天的销售数量如下表所示:
售价x/元 | 105 | 108 | 110 | 112 |
销售数量y/套 | 40 | 30 | 25 | 15 |
(1)根据上表,利用最小二乘法得到回归直线方程![]() ,求
,求![]() ;
;
(2)若售价为100元,则每天销售的套数约为多少(结果保留到整数)?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2017年10月18日至24日,中国共产党第十九次全国人民代表大会在北京顺利召开.大会期间,北京某高中举办了一次“喜迎十九大”的读书读报知识竞赛,参赛选手为从高一年级和高二年级随机抽取的各100名学生.图1和图2分别是高一年级和高二年级参赛选手成绩的频率分布直方图.
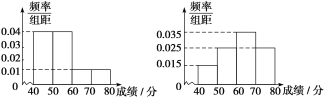
(1)分别计算参加这次知识竞赛的两个年级学生的平均成绩;
(2)若称成绩在68分以上的学生知识渊博,试以上述数据估计该高一、高二两个年级学生的知识渊博率;
(3)完成下面2×2列联表,并回答能否在犯错误的概率不超过0.010的前提下,认为高一、高二两个年级学生这次读书读报知识竞赛的成绩有差异.
分类 | 成绩低于60分人数 | 成绩不低于60分人数 | 总计 |
高一年级 | |||
高二年级 | |||
总计 |
附:
P(K2≥k) | 0.100 | 0.050 | 0.025 | 0.010 | 0.001 |
k | 2.706 | 3.841 | 5.024 | 6.635 | 10.828 |
K2=![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com