
分析 (1)由已知数列递推式求出数列首项,得到当n≥2时,an=Sn-Sn-1=-2SnSn-1,可得$\frac{1}{{S}_{n}}-\frac{1}{{S}_{n-1}}=2$,即数列{$\frac{1}{{S}_{n}}$}是以2为首项,公差为2 的等差数列.
(2)求出(1)中的等差数列得通项公式,得到Sn,再由已知数列递推式得an;
(3)求出${{S}_{n}}^{2}$,放缩后利用裂项相消法即可证得结论.
解答 (1)解:数列{$\frac{1}{{S}_{n}}$}是公差为2的等差数列.
证明:由已知有${S}_{1}={a}_{1}=\frac{1}{2}$,$\frac{1}{{S}_{1}}=2$;
当n≥2时,an=Sn-Sn-1=-2SnSn-1,
∴$\frac{1}{{S}_{n}}-\frac{1}{{S}_{n-1}}=2$,即数列{$\frac{1}{{S}_{n}}$}是以2为首项,公差为2 的等差数列.
(2)解:由(1)得:$\frac{1}{{S}_{n}}=2+2(n-1)=2n$,${S}_{n}=\frac{1}{2n}$.
当n≥2 时,${a}_{n}=-2{S}_{n}{S}_{n-1}=-\frac{1}{2n(n-1)}$.
当n=1 时,${a}_{1}=\frac{1}{2}$,
∴${a}_{n}=\left\{\begin{array}{l}{\frac{1}{2}(n=1)}\\{-\frac{1}{2n(n-1)}(n≥2)}\end{array}\right.$;
(3)证明:当n=1 时,${{S}_{1}}^{2}=\frac{1}{4}=\frac{1}{2}-\frac{1}{4×1}$成立.
当n≥2 时,${{S}_{1}}^{2}+{{S}_{2}}^{2}+{{S}_{3}}^{2}+…+{{S}_{n}}^{2}=\frac{1}{4}+$$\frac{1}{4×{2}^{2}}+\frac{1}{4×{3}^{2}}+…+\frac{1}{4{n}^{2}}$
=$\frac{1}{4}(1+\frac{1}{{2}^{2}}+\frac{1}{{3}^{2}}+…+\frac{1}{{n}^{2}})$<$\frac{1}{4}(1+\frac{1}{1×2}+\frac{1}{2×3}+…+\frac{1}{(n-1)n})$
=$\frac{1}{4}(1+1-\frac{1}{n})=\frac{1}{2}-\frac{1}{4n}$.
综上有${{S}_{1}}^{2}+{{S}_{2}}^{2}+{{S}_{3}}^{2}+…+{{S}_{n}}^{2}$$<\frac{1}{2}-\frac{1}{4n}$.
点评 本题考查数列递推式,考查等差关系的确定,训练了利用放缩法及裂项相消法证明数列不等式,属中档题.


科目:高中数学 来源: 题型:选择题
| A. | 从某工厂生产的3000件产品中抽取600件进行质量检验 | |
| B. | 从某工厂生产的两箱(每箱15件)产品中抽取6件进行质量检验 | |
| C. | 从甲、乙两厂生产的两箱(每箱15件)产品中抽取6件进行质量检验 | |
| D. | 从某厂生产的3000件产品中抽取10件进行质量检验 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
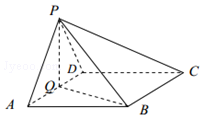 如图,在四棱锥P-ABCD中,底面ABCD为菱形,∠BAD=60°,Q为AD的中点.
如图,在四棱锥P-ABCD中,底面ABCD为菱形,∠BAD=60°,Q为AD的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com