
【题目】已知数列![]() 的前
的前![]() 项和为
项和为![]() ,且
,且![]() ,
,![]()
(1)求证:数列![]() 为等比数列,并求出数列
为等比数列,并求出数列![]() 的通项公式;
的通项公式;
(2)是否存在实数![]() ,对任意
,对任意![]() ,不等式
,不等式![]() 恒成立?若存在,求出
恒成立?若存在,求出![]() 的取值范围,若不存在请说明理由.
的取值范围,若不存在请说明理由.
【答案】(1)证明略;![]() (2)
(2)![]()
【解析】
(1)直接利用递推关系式求出数列的通项公式,进一步证明数列为等比数列;
(2)利用(1)的结论,进一步利用分组法和恒成立问题求出实数λ的取值范围.
证明:(1)已知数列{an}的前n项和为Sn,且![]() ,①
,①
当n=1时,![]() ,
,
则:当n≥2时,![]() ,②
,②
①﹣②得:an=2an﹣2an﹣1﹣![]() +
+![]() ,
,
整理得:![]() ,
,
所以:![]() ,
,
故: (常数),
(常数),
故:数列{an}是以![]() 为首项,2为公比的等比数列.
为首项,2为公比的等比数列.
故:![]() ,
,
所以:![]() .
.
由于:![]() ,
,
所以:![]() (常数).
(常数).
故:数列{bn}为等比数列.
(2)由(1)得:![]() ,
,
所以:![]() +(
+(![]() ),
),
=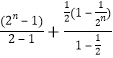 ,
,
=![]() ,
,
假设存在实数λ,对任意m,n∈N*,不等式![]() 恒成立,
恒成立,
即:![]() ,
,
由于:![]() ,
,
故当m=1时,![]() ,
,
所以:![]() ,
,
当n=1时,![]() .
.
故存在实数λ,且![]() .
.


 名校提分一卷通系列答案
名校提分一卷通系列答案 课程达标测试卷闯关100分系列答案
课程达标测试卷闯关100分系列答案 新卷王期末冲刺100分系列答案
新卷王期末冲刺100分系列答案 全能闯关100分系列答案
全能闯关100分系列答案科目:高中数学 来源: 题型:
【题目】如图,海岛O上有一座海拔300m的山,山顶上设有一个观察站A.上午11时测得一轮船在岛北偏东![]() 的B处,俯角为
的B处,俯角为![]() ;11时20分又测得该船在岛的北偏西
;11时20分又测得该船在岛的北偏西![]() 的C处,俯角为
的C处,俯角为![]() .
.

(1)该船的速度为每小时多少千米?
(2)若此船以不变的航速继续前进,则它何时到达岛的正西方向?此时船离开岛多少千米?(精确到lm)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】西北某省会城市计划新修一座城市运动公园,设计平面如图所示:其为五边形![]() ,其中三角形区域
,其中三角形区域![]() 为球类活动场所;四边形
为球类活动场所;四边形![]() 为文艺活动场所,
为文艺活动场所,![]() ,为运动小道(不考虑宽度)
,为运动小道(不考虑宽度)![]() ,
,![]() ,
,![]() 千米.
千米.
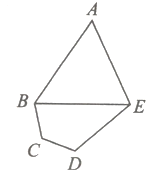
(1)求小道![]() 的长度;
的长度;
(2)求球类活动场所![]() 的面积最大值.
的面积最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设A、B、C、D为空间四个不共面的点,以![]() 的概率在每对点之间连一条边,任意两对点之间是否连边是相互独立的,则点A与B可用(一条边或者若干条边组成的)空间折线连接的概率为_______.
的概率在每对点之间连一条边,任意两对点之间是否连边是相互独立的,则点A与B可用(一条边或者若干条边组成的)空间折线连接的概率为_______.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 为偶函数.
为偶函数.
(1)求实数![]() 的值;
的值;
(2)若不等式![]() 恒成立,求实数a的取值范围;
恒成立,求实数a的取值范围;
(3)若函数![]() ,
,![]() ,是否存在实数m,使得
,是否存在实数m,使得![]() 的最小值为2,若存在,请求出m的值;若不存在,请说明理由.
的最小值为2,若存在,请求出m的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某超市为了解顾客的购物量及结算时间等信息,安排一名员工随机收集了在该超市购物的100名顾客的相关数据,如下表所示:
已知这100位顾客中一次性购物超过8件的顾客占55%.
一次性购物 | 1至4件 | 5至8件 | 9至12件 | 13至16件 | 17件及以上 |
顾客数(人) |
| 30 | 25 |
| 10 |
结算时间(分/人) | 1 | 1.5 | 2 | 2.5 | 3 |
(1)求![]() ,
,![]() 的值;
的值;
(2)求一位顾客一次购物的结算时间超过2分钟的概率(频率代替概率).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com