
【题目】假设你有一笔资金,现有三种投资方案,这三种方案的回报如下:
方案一:每天回报40元;
方案二:第一天回报10元,以后每天比前一天多回报10元;
方案三:第一天回报0.4元,以后每天的回报比前一天翻一番.
现打算投资10天,三种投资方案的总收益分别为![]() ,
,![]() ,
,![]() ,则( )
,则( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】在贯彻中共中央国务院关于精准扶贫政策的过程中,某单位定点帮扶甲、乙两个村各50户贫困户.为了做到精准帮扶,工作组对这100户村民的年收入情况、劳动能力情况、子女受教育情况、危旧房情况、患病情况等进行调查,并把调查结果转化为各户的贫困指标![]() 和
和![]() ,制成下图,其中“
,制成下图,其中“![]() ”表示甲村贫困户,“
”表示甲村贫困户,“![]() ”表示乙村贫困户.
”表示乙村贫困户.
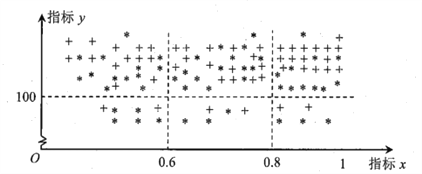
若![]() ,则认定该户为“绝对贫困户”,若
,则认定该户为“绝对贫困户”,若![]() ,则认定该户为“相对贫困户”,若
,则认定该户为“相对贫困户”,若![]() ,则认定该户为“低收入户”;
,则认定该户为“低收入户”;
若![]() ,则认定该户为“今年能脱贫户”,否则为“今年不能脱贫户”.
,则认定该户为“今年能脱贫户”,否则为“今年不能脱贫户”.
(1)从甲村50户中随机选出一户,求该户为“今年不能脱贫的绝对贫困户”的概率;
(2)若从所有“今年不能脱贫的非绝对贫困户”中选3户,用![]() 表示所选3户中乙村的户数,求
表示所选3户中乙村的户数,求![]() 的分布列和数学期望
的分布列和数学期望![]() ;
;
(3)试比较这100户中,甲、乙两村指标![]() 的方差的大小(只需写出结论).
的方差的大小(只需写出结论).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】根据国家环保部新修订的《 环境空气质量标准》规定:居民区![]() 的年平均浓度不得超过
的年平均浓度不得超过![]() 微克/立方米,
微克/立方米,![]() 的
的![]() 小时平均浓度不得超过
小时平均浓度不得超过![]() 微克/立方米.我市环保局随机抽取了一居民区
微克/立方米.我市环保局随机抽取了一居民区![]() 年
年![]() 天
天![]() 的
的![]() 小时平均浓度(单位:微克/立方米)的监测数据,数据统计如下表:
小时平均浓度(单位:微克/立方米)的监测数据,数据统计如下表:
组别 |
| 频数(天) | 频率 |
第一组 |
|
|
|
第二组 |
|
|
|
第三组 |
|
|
|
第四组 |
|
|
|
(1)这![]() 天的测量结果按上表中分组方法绘制成的样本频率分布直方图如图.
天的测量结果按上表中分组方法绘制成的样本频率分布直方图如图.

①求图中![]() 的值;
的值;
②求样本平均数,并根据样本估计总体的思想,从![]() 的年平均浓度考虑,判断该居民区的环境质量是否需要改善?并说明理由;
的年平均浓度考虑,判断该居民区的环境质量是否需要改善?并说明理由;
(2)将频率视为概率,对于![]() 年的某
年的某![]() 天,记这
天,记这![]() 天中该居民区
天中该居民区![]() 的
的![]() 小时平均浓度符合环境空气质量标准的天数为
小时平均浓度符合环境空气质量标准的天数为![]() ,求
,求![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】小明家的晚报在下午![]() 任何一个时间随机地被送到,他们一家人在下午
任何一个时间随机地被送到,他们一家人在下午![]() 任何一个时间随机地开始晚餐.为了计算晚报在晚餐开始之前被送到的概率,某小组借助随机数表的模拟方法来计算概率,他们的具体做法是将每个1分钟的时间段看作个体进行编号,
任何一个时间随机地开始晚餐.为了计算晚报在晚餐开始之前被送到的概率,某小组借助随机数表的模拟方法来计算概率,他们的具体做法是将每个1分钟的时间段看作个体进行编号,![]() 编号为01,
编号为01,![]() 编号为02,依此类推,
编号为02,依此类推,![]() 编号为90.在随机数表中每次选取一个四位数,前两位表示晚报时间,后两位表示晚餐时间,如果读取的四位数表示的晚报晚餐时间有一个不符合实际意义,视为这次读取的无效数据(例如下表中的第一个四位数7840中的78不符合晚报时间).按照从左向右,读完第一行,再从左向右读第二行的顺序,读完下表,用频率估计晚报在晚餐开始之前被送到的概率为
编号为90.在随机数表中每次选取一个四位数,前两位表示晚报时间,后两位表示晚餐时间,如果读取的四位数表示的晚报晚餐时间有一个不符合实际意义,视为这次读取的无效数据(例如下表中的第一个四位数7840中的78不符合晚报时间).按照从左向右,读完第一行,再从左向右读第二行的顺序,读完下表,用频率估计晚报在晚餐开始之前被送到的概率为![]()
![]()
7840 1160 5054 3139 8082 7732 5034 3682 4829 4052 |
4201 6277 5678 5188 6854 0200 8650 7584 0136 7655 |
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某房地产商建有三栋楼宇![]() ,三楼宇间的距离都为2千米,拟准备在此三楼宇围成的区域
,三楼宇间的距离都为2千米,拟准备在此三楼宇围成的区域![]() 外建第四栋楼宇
外建第四栋楼宇![]() ,规划要求楼宇
,规划要求楼宇![]() 对楼宇
对楼宇![]() ,
,![]() 的视角为
的视角为![]() ,如图所示,假设楼宇大小高度忽略不计.
,如图所示,假设楼宇大小高度忽略不计.
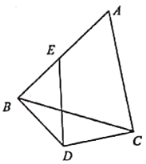
(1)求四栋楼宇围成的四边形区域![]() 面积的最大值;
面积的最大值;
(2)当楼宇![]() 与楼宇
与楼宇![]() ,
,![]() 间距离相等时,拟在楼宇
间距离相等时,拟在楼宇![]() ,
,![]() 间建休息亭
间建休息亭![]() ,在休息亭
,在休息亭![]() 和楼宇
和楼宇![]() ,
,![]() 间分别铺设鹅卵石路
间分别铺设鹅卵石路![]() 和防腐木路
和防腐木路![]() ,如图,已知铺设鹅卵石路、防腐木路的单价分别为
,如图,已知铺设鹅卵石路、防腐木路的单价分别为![]() ,
,![]() (单位:元千米,
(单位:元千米,![]() 为常数).记
为常数).记![]() ,求铺设此鹅卵石路和防腐木路的总费用的最小值.
,求铺设此鹅卵石路和防腐木路的总费用的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】以平面直角坐标系的原点O为极点,x轴非负半轴为极轴,并在两种坐标系中取相同的长度单位,建立极坐标系.曲线![]() 的极坐标方程为
的极坐标方程为![]() ,曲线
,曲线![]() 的参数方程为
的参数方程为![]() ,(
,(![]() 为参数).
为参数).
(1)求曲线![]() 的直角坐标方程及
的直角坐标方程及![]() 的普通方程;
的普通方程;
(2)已知点PQ为曲线![]() 与曲线
与曲线![]() 的交点,W为参数方程
的交点,W为参数方程![]() (
(![]() 为参数)曲线
为参数)曲线![]() 上一点,求点W到直线
上一点,求点W到直线![]() 的距离d的最大值.
的距离d的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P﹣ABCD中,底面ABCD是边长为2的菱形,∠DAB=60°,AD⊥PD,点F为棱PD的中点.
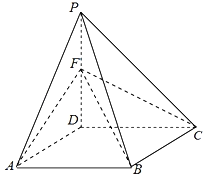
(1)在棱BC上是否存在一点E,使得CF∥平面PAE,并说明理由;
(2)若AC⊥PB,二面角D﹣FC﹣B的余弦值为![]() 时,求直线AF与平面BCF所成的角的正弦值.
时,求直线AF与平面BCF所成的角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】政府工作报告指出,2019年我国深入实施创新驱动发展战略,创新能力和效率进一步提升;2020年要提升科技支撑能力,健全以企业为主体的产学研一体化创新机制,某企业为了提升行业核心竞争力,逐渐加大了科技投入;该企业连续5年来的科技投入x(百万元)与收益y(百万元)的数据统计如下:
科技投入x | 1 | 2 | 3 | 4 | 5 |
收益y | 40 | 50 | 60 | 70 | 90 |
(1)请根据表中数据,建立y关于x的线性回归方程;
(2)按照(1)中模型,已知科技投入8百万元时收益为140百万元,求残差![]() (残差
(残差![]() 真实值-预报值).
真实值-预报值).
参考数据:回归直线方程![]() ,其中
,其中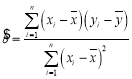 .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com