
| A. | [$\frac{3}{8}$,$\frac{11}{12}$]∪[$\frac{11}{8}$,$\frac{19}{12}$] | B. | ($\frac{1}{4}$,$\frac{5}{12}$]∪[$\frac{5}{8}$,$\frac{3}{4}$] | ||
| C. | [$\frac{3}{8}$,$\frac{7}{12}$]∪[$\frac{7}{8}$,$\frac{11}{12}$] | D. | ($\frac{1}{4}$,$\frac{3}{4}$]∪[$\frac{9}{8}$,$\frac{17}{12}$] |
分析 由题意可得,$\frac{T}{2}$=$\frac{π}{ω}$≥3π-2π=π,求得$\frac{1}{4}$<ω≤1,故排除A、D.检验当ω=$\frac{11}{12}$时,f(x)=$\sqrt{2}$sin($\frac{11}{12}$x-$\frac{π}{4}$)满足条件,故排除B,从而得出结论.
解答 解:f(x)=sinωx-cosωx=$\sqrt{2}$sin(ωx-$\frac{π}{4}$)(ω>$\frac{1}{4}$,x∈R),
若f(x)的任何一条对称轴与x轴交点的横坐标都不属于区间(2π,3π),
则$\frac{T}{2}$=$\frac{π}{ω}$≥3π-2π=π,ω≤1,即$\frac{1}{4}$<ω≤1,故排除A、D.
当ω=$\frac{11}{12}$时,f(x)=$\sqrt{2}$sin($\frac{11}{12}$x-$\frac{π}{4}$),
令$\frac{11}{12}$x-$\frac{π}{4}$=kπ+$\frac{π}{2}$,求得 x=$\frac{12}{11}$kπ+$\frac{9π}{11}$,可得函数f(x)的图象的对称轴为 x=$\frac{12}{11}$kπ+$\frac{9π}{11}$,k∈Z.
当k=1时,对称轴为 x=$\frac{21π}{11}$<2π,当k=2时,对称轴为 x=$\frac{33π}{11}$=3π,
满足条件:任何一条对称轴与x轴交点的横坐标都不属于区间(2π,3π),故排除B,
故选:C.
点评 本题主要考查正弦函数的图象的对称性和周期性,属于中档题.


 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案科目:高中数学 来源: 题型:选择题
| A. | $\frac{7}{25}$ | B. | $\frac{24}{25}$ | C. | -$\frac{24}{25}$ | D. | -$\frac{12}{25}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 224 | B. | 218 | C. | 228 | D. | 258 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{4}$ | B. | $\frac{1}{2}$ | C. | 1 | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
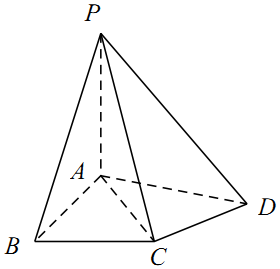 如图,在四棱锥P-ABCD中,△ABC为正三角形,AB⊥AD,AC⊥CD,PA=AC,PA⊥平面ABCD.
如图,在四棱锥P-ABCD中,△ABC为正三角形,AB⊥AD,AC⊥CD,PA=AC,PA⊥平面ABCD.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com