
ЁОЬтФПЁПїЛзгЃЌЙХДњжаЙњУёМфгщРжгУРДЭЖжРЕФВЉОпЃЌдчдкеНЙњЪБЦкОЭга.зюГЃМћЕФїЛзгЪЧе§СљУцЬхЃЌвВгае§ЪЎЫФУцЬхЁЂЧђаЮЪЎАЫУцЬхЕШаЮжЦЕФїЛзгЃЌШчЭМЪЧТњГЧККФЙГіЭСЕФЭмфЃЌЫќЪЧвЛИіЧђаЮЪЎАЫУцЬхїЛзгЃЌгаЪЎСљУцПЬзХвЛжСЪЎСљЪ§зжЃЌСэСНУцПЬЁАНОЁБКЭЁАОЦРДЁБЃЌЦфжаЁАНОЁББэЪОзюДѓЪ§ЪЎЦпЃЌЁАОЦРДЁББэЪОзюаЁЪ§СуЃЌУПЭЖвЛДЮЃЌГіЯжШЮКЮвЛИіЪ§зжЖМЪЧЕШПЩФмЕФ.ЯжЭЖжРЭмфШ§ДЮЙлВьЯђЩЯЕФЕуЪ§ЃЌдђетШ§ИіЪ§ФмЙЙГЩЙЋБШВЛЮЊ1ЕФЕШБШЪ§СаЕФИХТЪЮЊЃЈ ЃЉ

A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
ЁОД№АИЁПB
ЁОНтЮіЁП
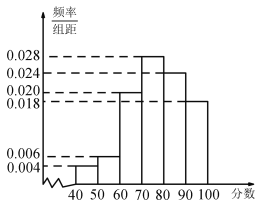
ЯШЧѓЫљгаЕФЛљБОЪТМўЕФзмЪ§ЃЌдйЭЈЙ§СаОйЗЈПЩЕУШ§ИіЪ§ФмЙЙГЩЙЋБШВЛЮЊ1ЕФЕШБШЪ§СаЕФЧщПіЙВга16жжЃЌДгЖјПЩЕУЫљЧѓЕФИХТЪ.
ЭЖжРЭмф3ДЮЙВга![]() ИіЛљБОЪТМўЃЌ
ИіЛљБОЪТМўЃЌ
ЦфжаетШ§ИіЪ§ФмЙЙГЩЙЋБШВЛЮЊ1ЕФЕШБШЪ§СаЕФЧщПігаЃЈШ§ИіЪ§гЩаЁЕНДѓХХСаЃЉЃК
1ЃЌ2ЃЌ4ЃЛ1ЃЌ3ЃЌ9ЃЛ1ЃЌ4ЃЌ16ЃЛ
2ЃЌ4ЃЌ8ЃЛ4ЃЌ6ЃЌ9ЃЛ3ЃЌ6ЃЌ12ЃЛ4ЃЌ8ЃЌ16ЃЛ9ЃЌ12ЃЌ16ЃЌ
ЙЪетШ§ИіЪ§ФмЙЙГЩЙЋБШВЛЮЊ1ЕФЕШБШЪ§СаЕФЧщПіЙВ![]() жжЃЌ
жжЃЌ
ЫљвдЫљЧѓИХТЪЮЊ![]() .
.
ЙЪбЁЃКB.



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊЪ§Са{an}ЕФЧАnЯюКЭSnЃНn2+pnЃЌЧвa4ЃЌa7ЃЌa12ГЩЕШБШЪ§СаЃЎ
ЃЈ1ЃЉЧѓЪ§Са{an}ЕФЭЈЯюЙЋЪНЃЛ
ЃЈ2ЃЉШєbn![]() ЃЌЧѓЪ§Са{bn}ЕФЧАnЯюКЭTnЃЎ
ЃЌЧѓЪ§Са{bn}ЕФЧАnЯюКЭTnЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФГЕчбЖЦѓвЕЮЊСЫСЫНтФГЕиЧјОгУёЖдЕчбЖЗўЮёжЪСПЦРМлЧщПіЃЌЫцЛњЕїВщ100 УћгУЛЇЃЌИљОнет100УћгУЛЇЖдИУЕчбЖЦѓвЕЕФЦРЗжЃЌЛцжЦЦЕТЪЗжВМжБЗНЭМЃЌШчЭМЫљЪОЃЌЦфжабљБОЪ§ОнЗжзщЮЊ![]() ЃЌ
ЃЌ![]() ЃЌЁЁ
ЃЌЁЁ![]() .
.
ЃЈ1ЃЉЙРМЦИУЕиЧјгУЛЇЖдИУЕчбЖЦѓвЕЦРЗжВЛЕЭгк70ЗжЕФИХТЪЃЌВЂЙРМЦЖдИУЕчбЖЦѓвЕЦРЗжЕФжаЮЛЪ§ЃЛ
ЃЈ2ЃЉЯжДгЦРЗждк![]() ЕФЕїВщгУЛЇжаЫцЛњГщШЁ2ШЫЃЌЧѓ2ШЫЦРЗжЖМдк
ЕФЕїВщгУЛЇжаЫцЛњГщШЁ2ШЫЃЌЧѓ2ШЫЦРЗжЖМдк![]() ЕФИХТЪ.
ЕФИХТЪ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁП2019Фъ11дТ26ШеЃЌСЊКЯЙњНЬПЦЮФзщжЏаћВМ3дТ14ШеЮЊЁАЙњМЪЪ§бЇШеЁБЃЈъЧГЦЃК![]() ЃЉЃЌ2020Фъ3дТ14ШеЪЧЕквЛИіЁАЙњМЪЪ§бЇШеЁБЃЎдВжмТЪ
ЃЉЃЌ2020Фъ3дТ14ШеЪЧЕквЛИіЁАЙњМЪЪ§бЇШеЁБЃЎдВжмТЪ![]() ЪЧдВЕФжмГЄгыжБОЖЕФБШжЕЃЌЪЧвЛИідкЪ§бЇМАЮяРэбЇжаЦеБщДцдкЕФЪ§бЇГЃЪ§ЃЎ
ЪЧдВЕФжмГЄгыжБОЖЕФБШжЕЃЌЪЧвЛИідкЪ§бЇМАЮяРэбЇжаЦеБщДцдкЕФЪ§бЇГЃЪ§ЃЎ![]() гааэЖрЦцУюаджЪЃЌШчРГВМФсзШКуЕШЪН
гааэЖрЦцУюаджЪЃЌШчРГВМФсзШКуЕШЪН![]() ЃЌМДЮЊе§ЦцЪ§ЕЙЪ§е§ИКНЛДэЯрМгЕШЃЎаЁКьЩшМЦСЫШчЭМЫљЪОЕФГЬађПђЭМЃЌвЊЧѓЪфГіЕФ
ЃЌМДЮЊе§ЦцЪ§ЕЙЪ§е§ИКНЛДэЯрМгЕШЃЎаЁКьЩшМЦСЫШчЭМЫљЪОЕФГЬађПђЭМЃЌвЊЧѓЪфГіЕФ![]() жЕгы
жЕгы![]() ЗЧГЃНќЫЦЃЌдђЂйЁЂЂкжаЗжБ№ЬюШыЕФПЩвдЪЧЃЈ ЃЉ
ЗЧГЃНќЫЦЃЌдђЂйЁЂЂкжаЗжБ№ЬюШыЕФПЩвдЪЧЃЈ ЃЉ
A.![]() ЃЌ
ЃЌ![]() B.
B.![]() ЃЌ
ЃЌ![]()
C.![]() ЃЌ
ЃЌ![]() D.
D.![]() ЃЌ
ЃЌ![]()
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЩшКЏЪ§fЃЈxЃЉЃН|xЉa|+|x+b|ЃЌabЃО0.
ЃЈ1ЃЉЕБaЃН1ЃЌbЃН1ЪБЃЌЧѓВЛЕШЪНfЃЈxЃЉЃМ3ЕФНтМЏЃЛ
ЃЈ2ЃЉШєfЃЈxЃЉЕФзюаЁжЕЮЊ2ЃЌЧѓ![]() ЕФзюаЁжЕ.
ЕФзюаЁжЕ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПбЁао4-5ЃКВЛЕШЪНбЁНВ
вбжЊКЏЪ§![]() .
.
ЃЈЂёЃЉНтВЛЕШЪНЃК ![]() ЃЛ
ЃЛ
ЃЈЂђЃЉЕБ![]() ЪБЃЌКЏЪ§
ЪБЃЌКЏЪ§![]() ЕФЭМЯѓгы
ЕФЭМЯѓгы![]() жсЮЇГЩвЛИіШ§НЧаЮЃЌЧѓЪЕЪ§
жсЮЇГЩвЛИіШ§НЧаЮЃЌЧѓЪЕЪ§![]() ЕФШЁжЕЗЖЮЇ.
ЕФШЁжЕЗЖЮЇ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌвбжЊЫФРтзЖ![]() ЃЌЕзУц
ЃЌЕзУц![]() ЮЊЦНааЫФБпаЮЃЌЧв
ЮЊЦНааЫФБпаЮЃЌЧв![]() ЃЌЕуMЮЊ
ЃЌЕуMЮЊ![]() ЕФжаЕуЃЌ
ЕФжаЕуЃЌ![]() ЃЌЧвЦНУц
ЃЌЧвЦНУц![]() ЦНУц
ЦНУц![]() .
.
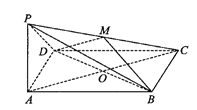
ЃЈ1ЃЉЧѓжЄЃКЦНУц![]() ЦНУц
ЦНУц![]() ЃЛ
ЃЛ
ЃЈ2ЃЉЕБжБЯп![]() гыЦНУц
гыЦНУц![]() ЫљГЩНЧЕФе§ЧажЕЮЊ
ЫљГЩНЧЕФе§ЧажЕЮЊ![]() ЪБЃЌЧѓЫФРтзЖ
ЪБЃЌЧѓЫФРтзЖ![]() ЕФЬхЛ§МАЦНУц
ЕФЬхЛ§МАЦНУц![]() НЋЫФРтзЖЗжГЩЕФСНВПЗжЕФЬхЛ§БШ.
НЋЫФРтзЖЗжГЩЕФСНВПЗжЕФЬхЛ§БШ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊКЏЪ§![]() Тњзу
Тњзу![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЎ
ЃЎ
ЃЈ1ЃЉЧѓКЏЪ§![]() ЕФНтЮіЪНЃЛ
ЕФНтЮіЪНЃЛ
ЃЈ2ЃЉЧѓКЏЪ§![]() ЕФЕЅЕїЧјМфЃЛ
ЕФЕЅЕїЧјМфЃЛ
ЃЈ3ЃЉЕБ![]() Чв
Чв![]() ЪБЃЌЧѓжЄЃК
ЪБЃЌЧѓжЄЃК![]() ЃЎ
ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПздгЩЙКЪЧвЛжжЭЈЙ§зджњНсЫуЙКЮяЕФаЮЪНЃЎФГДѓаЭГЌЪаЮЊЕїВщЙЫПЭздгЩЙКЕФЪЙгУЧщПіЃЌЫцЛњГщШЁСЫ100ШЫЃЌЕїВщНсЙћећРэШчЯТЃК
20вдЯТ | [20ЃЌ30ЃЉ | [30ЃЌ40ЃЉ | [40ЃЌ50ЃЉ | [50ЃЌ60ЃЉ | [60ЃЌ70] | 70вдЩЯ | |
ЪЙгУШЫЪ§ | 3 | 12 | 17 | 6 | 4 | 2 | 0 |
ЮДЪЙгУШЫЪ§ | 0 | 0 | 3 | 14 | 36 | 3 | 0 |
ЃЈ1ЃЉЯжЫцЛњГщШЁ1УћЙЫПЭЃЌЪдЙРМЦИУЙЫПЭФъСфдк[30ЃЌ50ЃЉЧвЮДЪЙгУздгЩЙКЕФИХТЪЃЛ
ЃЈ2ЃЉДгБЛГщШЁЕФФъСфдк[50ЃЌ70]ЪЙгУЕФздгЩЙКЙЫПЭжаЃЌЫцЛњГщШЁ2ШЫНјвЛВНСЫНтЧщПіЃЌЧѓет2ШЫФъСфЖМдк[50ЃЌ60ЃЉЕФИХТЪЃЛ
ЃЈ3ЃЉЮЊЙФРјЙЫПЭЪЙгУздгЩЙКЃЌИУГЌЪаФтЖдЪЙгУздгЩЙКЙЫПЭдљЫЭ1ИіЛЗБЃЙКЮяДќЃЎШєФГШеИУГЌЪадЄМЦга5000ШЫЙКЮяЃЌЪдЙРМЦИУГЌЪаЕБЬьжСЩйгІзМБИЖрЩйИіЛЗБЃЙКЮяДќЃП
ВщПДД№АИКЭНтЮі>>
АйЖШжТаХ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com