
| A. | y=$\sqrt{{x}^{2}}$和y=($\sqrt{x}$)2 | B. | y=lg(x2-1)和y=lg(x+1)+lg(x-1) | ||
| C. | y=logax2和y=2logax | D. | y=x和y=logaax |
分析 根据两个函数的定义域相同,对应关系也相同,即可判断它们是同一函数.
解答 解:对于A,y=$\sqrt{{x}^{2}}$=|x|(x∈R),与y=${(\sqrt{x})}^{2}$=x(x≥0)的定义域不同,对应关系也不同,不是同一个函数;
对于B,y=lg(x2-1)=(x<-1或x>1),与y=lg(x+1)+lg(x-1)=lg(x2-1)(x>1)的定义域不同,不是同一个函数;
对于C,y=logax2=2loga|x|(x≠0),与y=2logax(x>0)的定义域不同,对应关系也不同,不是同一个函数;
对于D,y=x(x∈R)y=logaax=x(x∈R)的定义域相同,对应关系也相同,是同一个函数.
故选:D.
点评 本题考查了判断两个函数是否为同一个函数的应用问题,是基础题目.


 期末宝典单元检测分类复习卷系列答案
期末宝典单元检测分类复习卷系列答案科目:高中数学 来源: 题型:选择题
| A. | 若m∥α,m∥β,则α∥β | B. | 若m∥n,m∥α,则n∥α | ||
| C. | 若α⊥β,m⊥α,n⊥β,则m⊥n | D. | 若α⊥β,m⊥α,n∥β,则m∥n |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a<b<c | B. | a<c<b | C. | c<a<b | D. | c<b<a |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-2,-1) | B. | (2,5) | C. | (-2,-1] | D. | (-∞,2)∪[5,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
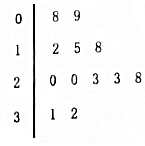 广安市2015年每个月平均气温(摄氏度)数据茎叶图如图,则这组数据的中位数、众数分别是( )
广安市2015年每个月平均气温(摄氏度)数据茎叶图如图,则这组数据的中位数、众数分别是( )| A. | 20;23 | B. | 21.5;20,23 | C. | 20;20,23 | D. | 21.5;23 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com