解答:
证明:(1)方法一:取CE的中点N,连接BN,如图1所示.
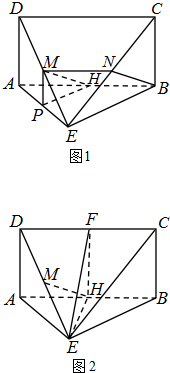
∵△CDE中,M、N分别是DE、CE的中点,∴MN∥CD且MN=
CD.
在矩形ABCD中,∵H是AB的中点,∴BH∥CD且BH=
CD,
∴MN∥BH且MN=BH,从而四边形BHMN为平行四边形,∴MH∥BN.
又∵MH?平面BCE,BN?平面BCE,∴MH∥平面BCE.
方法二:取AE的中点P,连接MP、HP,
在△ABE中,∵P、H分别是AE、AB的中点,∴HP∥BE,
∵HP?平面BCE,BE?平面BCE,∴HP∥平面BCE;同理有MP∥平面BCE,
又∵MP∩HP=P,∴平面MPH∥平面BCE,
∵MH?平面MPH,∴MH∥平面BCE.
(2)取CD中点F,连接EH、EF、FH,如图2所示,则在矩形ABCD中,FH⊥AB,FH=AD=2.
在△ABE中,AE=BE=2,∴EH⊥AB,∵FH∩EH=H,∴AB⊥平面EFH,
∵平面ABCD⊥平面ABE,∴∠EHF=90°,
∴Rt△EFH的面积等于几何体E-ABCD左(侧)视图的面积,
得
EH×FH=EH×2=,即
EH=,
∴在ABE中,有AH
2+EH
2=BH
2+EH
2=AE
2=DE
2=2
2,得
AH=BH=,从而
AB=2.
由AE
2+BE
2=AB
2=8知,AE⊥BE.
∵平面ABCD⊥平面ABE,四边形ABCD是矩形,∴AD⊥平面ABE,
又∵BE?平面ABE,∴AD⊥BE,而AD∩AE=A,∴BE⊥平面ADE,
∵BE?平面BCE,∴平面ADE⊥平面BCE.

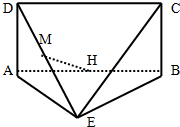 已知平面ABCD⊥平面ABE,四边形ABCD是矩形,AD=AE=BE=2,M、H分别是DE、AB的中点,主(正)视图方向垂直平面ABCD时,左(侧)视图的面积为
已知平面ABCD⊥平面ABE,四边形ABCD是矩形,AD=AE=BE=2,M、H分别是DE、AB的中点,主(正)视图方向垂直平面ABCD时,左(侧)视图的面积为


 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案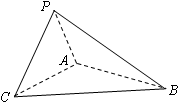 如图,平面PAC⊥平面ABC,△PAC是正三角形,∠CAB=90°,AB=2AC.
如图,平面PAC⊥平面ABC,△PAC是正三角形,∠CAB=90°,AB=2AC.