
【题目】已知a>0,b>0,a+b=4,m∈R.
(1)求![]() +
+![]() 的最小值;
的最小值;
(2)若|x+m|![]() |x
|x![]() 2|≤
2|≤![]() +
+![]() 对任意的实数x恒成立,求m的范围.
对任意的实数x恒成立,求m的范围.
【答案】(1)1;(2)-3≤m≤1
【解析】
(1)结合条件构造均值定理的结构形式,利用均值定理求解最小值;
(2)根据第(1)问可得![]() +
+![]() 的最小值,求|x+m|
的最小值,求|x+m|![]() |x
|x![]() 2|的最大值小于等于
2|的最大值小于等于![]() +
+![]() 的最小值.
的最小值.
(1)∵a>0,b>0,a+b=4,
∴![]() +
+![]() =(
=(![]() +
+![]() )
)![]() (a+b)=
(a+b)=![]() (2+
(2+![]() +
+![]() )≥
)≥![]() (2+2
(2+2![]() )=1,
)=1,
当且仅当a=b=2时取“=”;∴![]() +
+![]() 的最小值为1;
的最小值为1;
(2)若|x+m|![]() |x-2|≤
|x-2|≤![]() +
+![]() 对任意的实数x恒成立,
对任意的实数x恒成立,
则|x+m|![]() |x-2|≤
|x-2|≤![]() 对任意的实数x恒成立,
对任意的实数x恒成立,
即|x+m|![]() |x-2|≤1对任意的实数x恒成;
|x-2|≤1对任意的实数x恒成;
∵|x+m|![]() |x-2|≤|(x+m)
|x-2|≤|(x+m)![]() (x-2)|=|m+2|,
(x-2)|=|m+2|,
即|m+2|≤1,∴-1≤m+2≤1,解得![]() 3≤m≤
3≤m≤![]() 1,
1,
∴m的取值范围是![]() 3≤m≤
3≤m≤![]() 1.
1.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的两个焦点分别为
的两个焦点分别为![]() 、
、![]() ,
,![]() ,点
,点![]() 在椭圆上,且
在椭圆上,且![]() 的周长为
的周长为![]()
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)若点![]() 的坐标为
的坐标为![]() ,不过原点
,不过原点![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 相交于
相交于![]() ,
,![]() 两点,设线段
两点,设线段![]() 的中点为
的中点为![]() ,点
,点![]() 到直线
到直线![]() 的距离为
的距离为![]() ,且
,且![]() ,
,![]() ,
,![]() 三点共线,求
三点共线,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】4月23日是“世界读书日”,某中学在此期间开展了一系列的读书教育活动,为了解本校学生课外阅读情况,学校随机抽取了100名学生对其课外阅读时间进行调查,下图是根据调查结果绘制的学生日均课外阅读时间(单位:分钟)的频率分布直方图,若将日均课外阅读时间不低于60分钟的学生称为“读书谜”,低于60分钟的学生称为“非读书谜”.
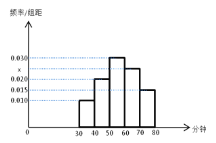
(1)求![]() 的值并估计全校3000名学生中读书谜大概有多少名?(将频率视为概率)
的值并估计全校3000名学生中读书谜大概有多少名?(将频率视为概率)
(2)根据已知条件完成下面![]() 的列联表,并据此判断是否有
的列联表,并据此判断是否有![]() 的把握认为“读书谜”与性别有关?
的把握认为“读书谜”与性别有关?
非读书迷 | 读书迷 | 合计 | |
男 | 40 | ||
女 | 25 | ||
合计 |
附: ,
,![]() .
.
| 0.100 | 0.050 | 0.025 | 0.010 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校为了推动数学教学方法的改革,学校将高一年级部分生源情况基本相同的学生分成甲乙两个班,每班各40人,甲班按原有模式教学,乙班实施教学方法改革.经过一年的教学实验,将甲乙两个班学生一年来的数学成绩取平均数,两个班学生的平均成绩均在![]() ,按照区间
,按照区间![]() ,
,![]() ,
,![]() 进行分组,绘制成如下频率分布直方图,规定不低于80分(百分制)为优秀.
进行分组,绘制成如下频率分布直方图,规定不低于80分(百分制)为优秀.
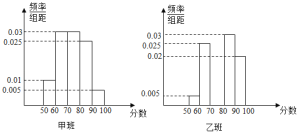
(1)完成表格,并判断是否有90%以上的把握认为“数学成绩优秀与教学改革有关”;
甲班 | 乙班 | 总计 | |
大于等于80分的人数 | |||
小于80分的人数 | |||
总计 |
(2)从乙班![]() 分数段中,按分层抽样随机抽取7名学生座谈,从中选三位同学发言,记来自
分数段中,按分层抽样随机抽取7名学生座谈,从中选三位同学发言,记来自![]() 发言的人数为随机变量
发言的人数为随机变量![]() ,求
,求![]() 的分布列和期望.附:
的分布列和期望.附: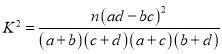 ,
,
| 0.10 | 0.05 | 0.025 |
| 2.706 | 3.841 | 5.024 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“一本书,一碗面,一条河,一座桥”曾是兰州的城市名片,而现在“兰州马拉松”又成为了兰州的另一张名片,随着全民运动健康意识的提高,马拉松运动不仅在兰州,而且在全国各大城市逐渐兴起,参与马拉松训练与比赛的人口逐年增加.为此,某市对人们参加马拉松运动的情况进行了统计调查.其中一项调查是调查人员从参与马拉松运动的人中随机抽取200人,对其每周参与马拉松长跑训练的天数进行统计,得到以下统计表:
平均每周进行长跑训练天数 | 不大于2天 | 3天或4天 | 不少于5天 |
人数 | 30 | 130 | 40 |
若某人平均每周进行长跑训练天数不少于5天,则称其为“热烈参与者”,否则称为“非热烈参与者”.
(1)经调查,该市约有2万人参与马拉松运动,试估计其中“热烈参与者”的人数;
(2)根据上表的数据,填写下列2×2列联表,并通过计算判断是否能在犯错误的概率不超过0.01的前提下认为“热烈参与马拉松”与性别有关?
热烈参与者 | 非热烈参与者 | 合计 | |
男 | 140 | ||
女 | 55 | ||
合计 |
附:k2=![]() (n为样本容量)
(n为样本容量)
P(k2≥k0) | 0.500 | 0.400 | 0.250 | 0.150 | 0.100 | 0.050 | 0.025 | 0.010 | 0.005 | 0.001 |
k0 | 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】当前全世界人民越来越关注环境保护问题,某地某监测站点于2018年8月起连续n天监测空气质量指数(AQI),数据统计如下表:
空气质量指数(μg/m3) | [0,50] | (50,100] | (100,150] | (150,200] | (200,250] |
空气质量等级 | 优 | 良 | 轻度污染 | 中度污染 | 重度污染 |
天数 | 20 | 40 | m | 10 | 5 |
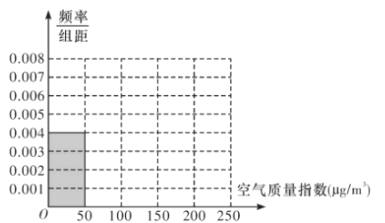
(1)根据所给统计表和频率分布直方图中的信息求出n,m的值,并完成频率分布直方图;
(2)由频率分布直方图,求该组数据的平均数与中位数;
(3)在空气质量指数分别为[0,50]和(50,100]的监测数据中,用分层抽样的方法抽取6天,从中任意选取2天,求事件A“两天空气质量等级都为良”发生的概率。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图四边形ABCD为菱形,G为AC与BD交点,面![]() 平面ABCD.
平面ABCD.
(1)证明:![]() 平面BDE;
平面BDE;
(2)若![]() 为等边三角形,
为等边三角形,![]() ,
,![]() ,三棱锥
,三棱锥![]() 的体积为
的体积为![]() ,求四棱锥
,求四棱锥![]() 的侧面积.
的侧面积.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的四个顶点组成的四边形的面积为
的四个顶点组成的四边形的面积为![]() ,且经过点
,且经过点 .
.

(1)求椭圆![]() 的方程;
的方程;
(2)若椭圆![]() 的下顶点为
的下顶点为![]() ,如图所示,点
,如图所示,点![]() 为直线
为直线![]() 上的一个动点,过椭圆
上的一个动点,过椭圆![]() 的右焦点
的右焦点![]() 的直线
的直线![]() 垂直于
垂直于![]() ,且与
,且与![]() 交于
交于![]() 两点,与
两点,与![]() 交于点
交于点![]() ,四边形
,四边形![]() 和
和![]() 的面积分别为
的面积分别为![]() .求
.求![]() 的最大值.
的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com