
【题目】已知数列![]() 满足
满足![]() ,
,![]() ,
,![]() .
.
(1)若![]() ,试问是否存在实数
,试问是否存在实数![]() ,使得数列
,使得数列![]() 是等比数列?若存在,求出
是等比数列?若存在,求出![]() 的值;若不存在,请说明理由;
的值;若不存在,请说明理由;
(2)在(1)的条件下,求数列![]() 的通项公式.
的通项公式.
科目:高中数学 来源: 题型:
【题目】某省确定从2021年开始,高考采用“![]() ”的模式,取消文理分科,即“3”包括语文、数学、外语,为必考科目;“1”表示从物理、历史中任选一门;“2”则是从生物、化学、地理、政治中选择两门,共计六门考试科目.某高中从高一年级2000名学生(其中女生900人)中,采用分层抽样的方法抽取
”的模式,取消文理分科,即“3”包括语文、数学、外语,为必考科目;“1”表示从物理、历史中任选一门;“2”则是从生物、化学、地理、政治中选择两门,共计六门考试科目.某高中从高一年级2000名学生(其中女生900人)中,采用分层抽样的方法抽取![]() 名学生进行调查.
名学生进行调查.
(1)已知抽取的![]() 名学生中含男生110人,求
名学生中含男生110人,求![]() 的值及抽取到的女生人数;
的值及抽取到的女生人数;
(2)学校计划在高二上学期开设选修中的“物理”和“历史”两个科目,为了了解学生对这两个科目的选课情况,对在(1)的条件下抽取到的n名学生进行问卷调查(假定每名学生在这两个科目中必须选择一个科目且只能选择一个科目).下表是根据调查结果得到的![]() 列联表,请将列联表补充完整,并判断是否有99.5%的把握认为选择科目与性别有关?
列联表,请将列联表补充完整,并判断是否有99.5%的把握认为选择科目与性别有关?
说明你的理由;

(3)在(2)的条件下,从抽取的选择“物理”的学生中按分层抽样抽取6人,再从这6名学生中抽取2人,对“物理”的选课意向作深入了解,求2人中至少有1名女生的概率.
附:![]() ,其中
,其中![]() .
.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】中国海军,正在以不可阻挡的气魄向深蓝进军。在中国海军加快建设的大背景下,国产水面舰艇吨位不断增大、技术日益现代化,特别是国产航空母舰下水,航母需要大量高素质航母舰载机飞行员。为此中国海军在全国9省9所优质普通高中进行海航班建设试点培育航母舰载机飞行员。2017年4月我省首届海军航空实验班开始面向全省遴选学员,有10000名初中毕业生踊跃报名投身国防,经过文化考试、体格测试、政治考核、心理选拔等过程筛选,最终招收50名学员。培养学校在关注学员的文化素养同时注重学员的身体素质,要求每月至少参加一次野营拉练活动(下面简称“活动”)并记录成绩.10月某次活动中海航班学员成绩统计如图所示:
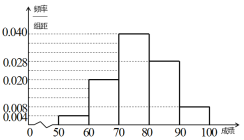
(Ⅰ)根据图表,试估算学员在活动中取得成绩的中位数(精确到![]() );
);
(Ⅱ)根据成绩从![]() 、
、![]() 两组学员中任意选出两人为一组,若选出成绩分差大于
两组学员中任意选出两人为一组,若选出成绩分差大于![]() ,则称该组为“帮扶组”,试求选出两人为“帮扶组”的概率.
,则称该组为“帮扶组”,试求选出两人为“帮扶组”的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某工厂利用辐射对食品进行灭菌消毒,现准备在该厂附近建一职工宿舍,并对宿舍进行防辐射处理,建房防辐射材料的选用与宿舍到工厂距离有关.若建造宿舍的所有费用p(万元)和宿舍与工厂的距离x(km)的关系为![]() ,若距离为1km时,测算宿舍建造费用为100万元.为了交通方便,工厂与宿舍之间还要修一条道路,已知购置修路设备需5万元,铺设路面每公里成本为6万元,设f(x)为建造宿舍与修路费用之和.
,若距离为1km时,测算宿舍建造费用为100万元.为了交通方便,工厂与宿舍之间还要修一条道路,已知购置修路设备需5万元,铺设路面每公里成本为6万元,设f(x)为建造宿舍与修路费用之和.
(1)求f(x)的表达式
(2)宿舍应建在离工厂多远处,可使总费用f(x)最小并求最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,以椭圆
,以椭圆![]() 的长轴和短轴为对角线的四边形的面积为
的长轴和短轴为对角线的四边形的面积为![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)若直线![]() 与椭圆
与椭圆![]() 相交于
相交于![]() ,
,![]() 两点,设
两点,设![]() 为椭圆
为椭圆![]() 上一动点,且满足
上一动点,且满足![]() (
(![]() 为坐标原点).当
为坐标原点).当![]() 时,求
时,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知F为椭圆C:![]() 的左焦点,过F作两条互相垂直的直线
的左焦点,过F作两条互相垂直的直线![]() ,
,![]() ,直线
,直线![]() 与C交于A,B两点,直线
与C交于A,B两点,直线![]() 与C交于D,E两点,则四边形ADBE的面积最小值为( )
与C交于D,E两点,则四边形ADBE的面积最小值为( )
A.4B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆C的圆心C在直线![]() 上,且与x轴正半轴相切,点C与坐标原点O的距离为
上,且与x轴正半轴相切,点C与坐标原点O的距离为![]() .
.
(1)求圆C的标准方程;
(2)直线l过点 ![]() 且与圆C相交于A,B两点,求弦长
且与圆C相交于A,B两点,求弦长![]() 的最小值及此时直线l的方程.
的最小值及此时直线l的方程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com