
【题目】已知函数![]() 和函数
和函数![]() ,关于这两个函数图像的交点个数,下列四个结论:①当
,关于这两个函数图像的交点个数,下列四个结论:①当![]() 时,两个函数图像没有交点;②当
时,两个函数图像没有交点;②当![]() 时,两个函数图像恰有三个交点;③当
时,两个函数图像恰有三个交点;③当![]() 时,两个函数图像恰有两个交点;④当
时,两个函数图像恰有两个交点;④当![]() 时,两个函数图像恰有四个交点.正确结论的个数为( )
时,两个函数图像恰有四个交点.正确结论的个数为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【答案】D
【解析】
由两个函数图像交点个数,转化为![]() 的解的个数,进而转化为
的解的个数,进而转化为![]() 的解的个数,令
的解的个数,令 ,利用导数求得函数单调性与最值,结合函数的性质,即可求解.
,利用导数求得函数单调性与最值,结合函数的性质,即可求解.
由题意,两个函数![]() 和函数
和函数![]() 图像交点个数,
图像交点个数,
即为方程![]() 的解的个数,即方程
的解的个数,即方程![]() 的解的个数,
的解的个数,
令 ,
,
①当![]() 时,函数
时,函数![]() ,则
,则![]() ,
,
所以![]() 在
在![]() 上为增函数,值域为
上为增函数,值域为![]() ;
;
②当![]() 时,
时,![]() ,
,![]() ,
,
由![]() ,得
,得![]() .
.
当![]() 时,
时,![]() ,
,![]() 为增函数;
为增函数;
当![]() 时,
时,![]() ,
,![]() 为减函数;
为减函数;
当![]() 时,
时,![]() ,
,
所以函数![]() 在
在![]() 上有最大值为
上有最大值为![]() ,
,
令![]() ,方程
,方程![]() ,化为
,化为![]() ,
,
当![]() 时,方程
时,方程![]() 无解,原方程无解,两个函数图像无交点;
无解,原方程无解,两个函数图像无交点;
当![]() 时,方程
时,方程![]() 有唯一解
有唯一解![]() ,
,![]() ,原方程有唯一解,
,原方程有唯一解,
两个函数图像恰有一个交点;
当![]() 时,方程
时,方程![]() 有两解
有两解![]() ,
,![]() ,原
,原
方程有两解,两个函数图像恰有两个交点;
当![]() 时,方程
时,方程![]() 有两解
有两解![]() ,
,![]() ,原方程有三解,两个函数图像恰有三个交点;
,原方程有三解,两个函数图像恰有三个交点;
当![]() 时,方程
时,方程![]() 有两解
有两解![]() ,
,![]() ,原方程有四解,两个函数图像恰有四个交点.
,原方程有四解,两个函数图像恰有四个交点.
故选D.



科目:高中数学 来源: 题型:
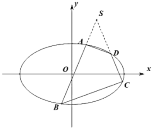
【题目】如图,在平面直角坐标系![]() 中,已知
中,已知![]() 分别是椭圆
分别是椭圆![]() :
:![]() (
(![]() )的左右焦点,点
)的左右焦点,点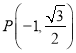 是椭圆
是椭圆![]() 上一点,且
上一点,且![]() .若椭圆
.若椭圆![]() 的内接四边形
的内接四边形![]() 的边
的边![]() 的延长线交于椭圆外一点
的延长线交于椭圆外一点![]() ,且点
,且点![]() 的横坐标为1,记直线
的横坐标为1,记直线![]() 的斜率分别为
的斜率分别为![]() ,
,![]() .
.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)若![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】从某小学的期末考试中抽取部分学生的数学成绩,由抽查结果得到如图的频率分布直方图,分数落在区间![]() ,
,![]() ,
,![]() 内的频率之比为
内的频率之比为![]() .
.
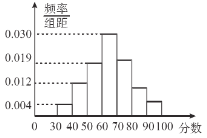
(1)求这些学生的分数落在区间![]() 内的频率;
内的频率;
(2)(ⅰ)若采用分层抽样的方法从分数落在区间![]() ,
,![]() 内抽取4人,求从分数落在区间
内抽取4人,求从分数落在区间![]() ,
,![]() 内各抽取的人数;
内各抽取的人数;
(ⅱ)从上述抽取的4人中再随机抽取2人,求这2人全部来自于区间![]() 内的概率.
内的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司准备将1000万元资金投人到市环保工程建设中,现有甲,乙两个建设项目选择,若投资甲项目一年后可获得的利润![]() (万元)的概率分布列如表所示:
(万元)的概率分布列如表所示:
| 110 | 120 | 170 |
|
| 0.4 |
|
且![]() 的期望
的期望![]() ;若投资乙项目一年后可获得的利润
;若投资乙项目一年后可获得的利润![]() (万元)与该项目建设材料的成本有关,在生产的过程中,公司将根据成本情况决定是否在第二和第三季度进行产品的价格调整,两次调整相互独立且调整的概率分别为
(万元)与该项目建设材料的成本有关,在生产的过程中,公司将根据成本情况决定是否在第二和第三季度进行产品的价格调整,两次调整相互独立且调整的概率分别为![]() 和
和![]() .若乙项目产品价格一年内调整次数
.若乙项目产品价格一年内调整次数![]() (次数)与
(次数)与![]() 的关系如表所示:
的关系如表所示:
| 0 | 1 | 2 |
| 41.2 | 117.6 | 204.0 |
(1)求![]() ,
,![]() 的值;
的值;
(2)求![]() 的分布列.
的分布列.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() :
:![]() ,其焦点到准线的距离为2.直线
,其焦点到准线的距离为2.直线![]() 与抛物线
与抛物线![]() 交于
交于![]() ,
,![]() 两点,过
两点,过![]() ,
,![]() 分别作抛物线
分别作抛物线![]() 的切线
的切线![]() 与
与![]() ,
,![]() 与
与![]() 交于点
交于点![]() .
.
(1)求抛物线![]() 的标准方程;
的标准方程;
(2)若![]() ,求
,求![]() 面积的最小值.
面积的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),将曲线
为参数),将曲线![]() 上各点纵坐标伸长到原来的
上各点纵坐标伸长到原来的![]() 倍(横坐标不变),得到曲线
倍(横坐标不变),得到曲线![]() .以坐标原点
.以坐标原点![]() 为极点,
为极点,![]() 轴的正半轴为极轴建立极坐标系,直线
轴的正半轴为极轴建立极坐标系,直线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)写出曲线![]() 的极坐标方程与直线
的极坐标方程与直线![]() 的直角坐标方程;
的直角坐标方程;
(2)曲线![]() 上是否存在不同的两点
上是否存在不同的两点![]() ,
,![]() (以上两点坐标均为极坐标,
(以上两点坐标均为极坐标,![]() ,
,![]() ,
,![]() ,
,![]() ),使点
),使点![]() 、
、![]() 到
到![]() 的距离都为
的距离都为![]() ?若存在,求出
?若存在,求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线![]() 与椭圆
与椭圆![]() 交于不同的两点
交于不同的两点![]() ,线段
,线段![]() 的中点为
的中点为![]() ,且直线
,且直线![]() 与直线
与直线![]() 的斜率之积为
的斜率之积为![]() .若直线
.若直线![]() 与直线
与直线![]() 交于点
交于点![]() ,与直线
,与直线![]() 交于点
交于点![]() ,且
,且![]() 点为直线
点为直线![]() 上一点.
上一点.
(1)求![]() 的轨迹方程;
的轨迹方程;
(2)若![]() 为椭圆
为椭圆![]() 的上顶点,直线
的上顶点,直线![]() 与
与![]() 轴交点
轴交点![]() ,记
,记![]() 表示面积,求
表示面积,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系xOy中,直线l过点![]() 且倾斜角为
且倾斜角为![]() .以坐标原点O为极点,x轴的正半轴为极轴建立极坐标系,已知曲线C的极坐标方程为
.以坐标原点O为极点,x轴的正半轴为极轴建立极坐标系,已知曲线C的极坐标方程为![]() ,l与C交于M,N两点.
,l与C交于M,N两点.
(1)求C的直角坐标方程和![]() 的取值范围;
的取值范围;
(2)求MN中点H的轨迹的参数方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2016年某高校艺术类考试中,共有6位选手参加,其中3位女生,3位男生,现这6名考生依次出场进行才艺展出,如果3位男生中任何2人都不能连续出场,且女生甲不能排第一个,那么这6名考生出场顺序的排法种数为( )
A.108B.120C.132D.144
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com