
| A. | $({-∞,-\frac{4}{3}}]∪[{0,+∞})$ | B. | $({-∞,-\frac{3}{4}}]∪[{0,+∞})$ | C. | $[{-\frac{3}{4},0}]$ | D. | $[{-\frac{4}{3},0}]$ |
分析 圆C是以C(-2,1)为圆心,r=1为半径的圆,$\frac{y}{x}$的最值就是求过原点与圆上一点连线斜率的最值,相切时有最值,由此能求出$\frac{y}{x}$的取值范围.
解答 解:实数x,y满足x2+y2+4x-2y+4=0,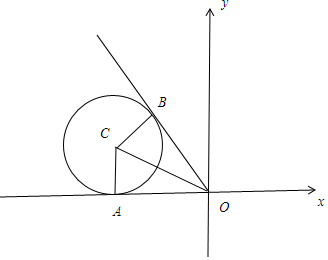
圆心C(-2,1),半径r=$\frac{1}{2}\sqrt{16+4-16}$=1,
如图,圆C是以C(-2,1)为圆心,
r=1为半径的圆,
过O作圆C的切线OA,OB,则OA=OB=2,
AC=BC=1,OC=$\sqrt{5}$,
tan∠AOC=$\frac{AC}{AO}$=$\frac{1}{2}$,
∴tan∠AOB=tan2∠AOC=$\frac{2×\frac{1}{2}}{1-(\frac{1}{2})^{2}}$=$\frac{4}{3}$,
∴kOB=-tan∠AOB=-$\frac{4}{3}$,kOA=0,
∵$\frac{y}{x}$的最值就是求过原点与圆上一点连线斜率的最值,相切时有最值,
∴$\frac{y}{x}$的取值范围是[-$\frac{4}{3}$,0].
故选:D.
点评 本题考查点的纵坐标与横坐标的比值的取值范围的求法,考查直线与圆的位置关系,考查推理论证能力、运算求解能力,考查转化化归思想、数形结合思想,是中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,-2] | B. | (-∞,-1] | C. | [1,+∞) | D. | [2,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ?x∈R,ex>0 | B. | ?x∈N,x2>0 | ||
| C. | ?x0∈R,lnx0<0 | D. | $?{x_0}∈{N^*},sin\frac{π}{2}{x_0}=1$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ∅ | B. | $\{x|\frac{1}{2}<x≤1\}$ | C. | {x|x<1} | D. | {x|0<x<1} |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com