
【题目】已知函数f(x)=|x﹣a|﹣|x﹣2|﹣1.
(1)当a=1时,求不等式f(x)≥0的解集;
(2)当f(x)≤1,求实数a的取值范围.
【答案】(1)[2,+∞);(2)0≤a≤4.
【解析】
(1)将函数写成分段函数的形式,画出函数图像,数形结合求得不等式解集;
(2)将恒成立问题转化为求解绝对值不等式的最值问题,再利用绝对值三角不等式求得最值即可.
(1)a=1时,
函数f(x)=|x﹣1|﹣|x﹣2|﹣1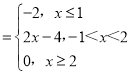 ;
;
画函数f(x)的图象,如图所示;
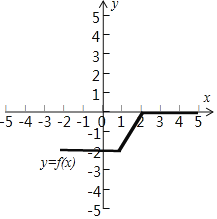
由图象知,不等式f(x)≥0的解集为[2,+∞);
(2)令f(x)≤1,得f(x)=|x﹣a|﹣|x﹣2|﹣1≤1,
即|x﹣a|﹣|x﹣2|≤2(*);
设g(x)=|x﹣a|﹣|x﹣2|,
则g(x)≤|(x﹣a)﹣(x﹣2)|=|﹣a+2|=|a﹣2|,
当且仅当![]() 时
时![]() ,或
,或![]() 时,
时,![]() 取得最大值.
取得最大值.
不等式(*)可化为|a﹣2|≤2,
即﹣2≤a﹣2≤2,
解得0≤a≤4;
所以实数a的取值范围是0≤a≤4.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】某保险公司对一个拥有20000人的企业推出一款意外险产品,每年每位职工只要交少量保费,发生意外后可一次性获得若干赔偿金,保险公司把企业的所有岗位共分为![]() 三类工种,从事这三类工种的人数分别为12000,6000,2000,由历史数据统计出三类工种的赔付频率如下表(并以此估计赔付概率):
三类工种,从事这三类工种的人数分别为12000,6000,2000,由历史数据统计出三类工种的赔付频率如下表(并以此估计赔付概率):
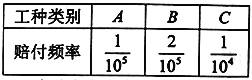
已知![]() 三类工种职工每人每年保费分别为25元、25元、40元,出险后的赔偿金额分别为100万元、100万元、50万元,保险公司在开展此项业务过程中的固定支出为每年10万元.
三类工种职工每人每年保费分别为25元、25元、40元,出险后的赔偿金额分别为100万元、100万元、50万元,保险公司在开展此项业务过程中的固定支出为每年10万元.
(1)求保险公司在该业务所或利润的期望值;
(2)现有如下两个方案供企业选择:
方案1:企业不与保险公司合作,职工不交保险,出意外企业自行拿出与保险公司提供的等额赔偿金赔偿付给意外职工,企业开展这项工作的固定支出为每年12万元;
方案2:企业与保险公司合作,企业负责职工保费的70%,职工个人负责保费的30%,出险后赔偿金由保险公司赔付,企业无额外专项开支.
请根据企业成本差异给出选择合适方案的建议.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点A(0,2),动点M到点A的距离比动点M到直线y=﹣1的距离大1,动点M的轨迹为曲线C.
(1)求曲线C的方程;
(2)Q为直线y=﹣1上的动点,过Q做曲线C的切线,切点分别为D、E,求△QDE的面积S的最小值
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】欲设计如图所示的平面图形,它由上、下两部分组成,其中上部分是弓形(圆心为![]() ,半径为
,半径为![]() ,
,![]() ,
,![]() ),下部分是矩形
),下部分是矩形![]() .
.
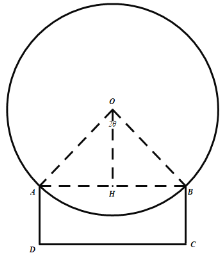
(1)若![]() ,求该平面图形的周长的最大值;
,求该平面图形的周长的最大值;
(2)若![]() ,试确定
,试确定![]() 的值,使得该平面图形的面积最大.
的值,使得该平面图形的面积最大.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校为了了解高一新生是否愿意参加军训,随机调查了80名新生,得到如下2×2列联表
愿意 | 不愿意 | 合计 | |
男 | x | 5 | M |
女 | y | z | 40 |
合计 | N | 25 | 80 |
(1)写出表中x,y,z,M,N的值,并判断是否有99.9%的把握认为愿意参加军训与性别有关;
(2)在被调查的不愿意参加军训的学生中,随机抽出3人,记这3人中男生的人数为ξ,求ξ的分布列和数学期望.
参考公式: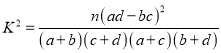
附:
P(K2≥k0) | 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.01 | 0.005 | 0.001 |
k0 | 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知矩形![]() 所在平面垂直于直角梯形
所在平面垂直于直角梯形![]() 所在平面,平面
所在平面,平面![]() 平面
平面![]() ,且
,且![]() ,且
,且![]() .
.

(1)设点![]() 为棱
为棱![]() 中点,在面
中点,在面![]() 内是否存在点
内是否存在点![]() ,使得
,使得![]() 平面
平面![]() ?若存在,请证明,若不存在,说明理由;
?若存在,请证明,若不存在,说明理由;
(2)求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的左、右焦点分别为
的左、右焦点分别为![]() ,
,![]() ,过点
,过点![]() 的直线与椭圆
的直线与椭圆![]() 交于
交于![]() 两点,延长
两点,延长![]() 交椭圆
交椭圆![]() 于点
于点![]() ,
,![]() 的周长为8.
的周长为8.

(1)求![]() 的离心率及方程;
的离心率及方程;
(2)试问:是否存在定点![]() ,使得
,使得![]() 为定值?若存在,求
为定值?若存在,求![]() ;若不存在,请说明理由.
;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某医科大学实习小组为研究实习地昼夜温差与患感冒人数之间的关系,分别到当地气象部门和某医院抄录了1月份至3月份每月5日、20日的昼夜温差情况与因患感冒而就诊的人数,得到如表资料:
日期 | 1月5日 | 1月20日 | 2月5日 | 2月20日 | 3月5日 | 3月20日 |
昼夜温差 | 10 | 11 | 13 | 12 | 8 | 6 |
就诊人数 | 22 | 25 | 29 | 26 | 16 | 12 |
该小组确定的研究方案是:先从这六组数据中随机选取4组数据求线性回归方程,再用剩余的2组数据进行检验.
(1)求剩余的2组数据都是20日的概率;
(2)若选取的是1月20日,2月5日,2月20日,3月5日四组数据.
①请根据这四组数据,求出![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() (
(![]() ,
,![]() 用分数表示);
用分数表示);
②若某日的昼夜温差为![]() ,预测当日就诊人数约为多少人?
,预测当日就诊人数约为多少人?
附参考公式: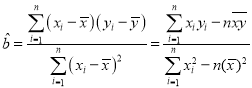 ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设![]() ,其中
,其中![]() .若
.若![]() 对一切
对一切![]() 恒成立,则①
恒成立,则①![]() ;②
;②![]() ;③
;③![]() 既不是奇函数也不是偶函数;④
既不是奇函数也不是偶函数;④![]() 的单调递增区间是
的单调递增区间是![]() ;⑤存在经过点
;⑤存在经过点![]() 的直线与函数
的直线与函数![]() 的图像不相交.以上结论正确的是________________.(写出所有正确结论的序号)
的图像不相交.以上结论正确的是________________.(写出所有正确结论的序号)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com