
【题目】已知椭圆C:![]() 的离心率为
的离心率为![]() ,与坐标轴分别交于A,B两点,且经过点Q(
,与坐标轴分别交于A,B两点,且经过点Q(![]() ,1).
,1).
(Ⅰ)求椭圆C的标准方程;
(Ⅱ)若P(m,n)为椭圆C外一动点,过点P作椭圆C的两条互相垂直的切线l1、l2,求动点P的轨迹方程,并求△ABP面积的最大值.
【答案】(Ⅰ)![]() 1;(Ⅱ)
1;(Ⅱ)![]() .
.
【解析】
(Ⅰ)由离心率及椭圆过的点的坐标,及a,b,c之间的关系可得a,b的值,进而求出椭圆的方程;
(Ⅱ)过P的两条切线分斜率存在和不存在两种情况讨论,当斜率不存在时,直接由椭圆的方程可得切点A,B的坐标,当切线的斜率存在且不为0时,设过P的切线方程,与椭圆联立.由判别式等于0可得参数的关系,进而可得PA,PB的斜率之积,进而可得m,n之间的关系,即P的轨迹方程,显然切线斜率不存在时的点P也在轨迹方程上;因为PA,PB互相垂直,所以三角形PAB的面积为S△ABP![]() |PA||PB|
|PA||PB|![]() ,当且仅当|PA|=|PB|时取等号,此时得到点P的坐标求解.
,当且仅当|PA|=|PB|时取等号,此时得到点P的坐标求解.
(Ⅰ)由题意可得e![]() ,
,![]() 1,c2=a2﹣b2,解得a2=4,b2=2,
1,c2=a2﹣b2,解得a2=4,b2=2,
所以椭圆的方程为:![]() 1;
1;
(Ⅱ)设两个切点分别为A,B,①当两条切线中有一条斜率不存在时,
即A,B两点分别位于椭圆的长轴和短轴的端点,此时P的坐标为:(±2,±![]() ),
),
②当两条切线的斜率存在且不为0时,设过P的切线的方程为:y﹣n=k(x﹣m),
联立直线y﹣n=k(x﹣m)和椭圆的方程 ,整理可得(1+2k2)x2﹣4k(km﹣n)x+2(km﹣n)2﹣4=0,
,整理可得(1+2k2)x2﹣4k(km﹣n)x+2(km﹣n)2﹣4=0,
由题意可得△=16k2(km﹣n)2﹣4(1+2k2)[2(km﹣n)2﹣4]=0,整理可得(m2﹣4)k2﹣2kmn+n2﹣2=0,所以k1k2![]() ,
,
设直线PA,PB的斜率分别为k1,k2,则k1k2![]() ,
,
而PA,PB互相垂直,所以![]() 1,
1,
即m2+n2=6,(m≠±2),
又因为P(±2,![]() )在m2+n2=6上,
)在m2+n2=6上,
所以点P在圆x+y2=6上.
因为l1⊥l2,
所以S△ABP![]() |PA||PB|
|PA||PB|![]() ,当且仅当|PA|=|PB|时取等号,
,当且仅当|PA|=|PB|时取等号,
即P在椭圆的短轴所在的直线上时即P(0,![]() ),
),
由圆及椭圆的对称性设P(0,![]() ),则直线PA的斜率为1,可得直线PA的方程为:y=x
),则直线PA的斜率为1,可得直线PA的方程为:y=x![]() ,
,
代入椭圆的方程可得3x2+4![]() x+8=0,解得x
x+8=0,解得x![]() ,y
,y![]() ,即A(
,即A(![]() ,
,![]() ),
),
所以|PA|![]() ,所以AB2=2|PA|2
,所以AB2=2|PA|2![]() ,
,
所以(S△ABP)max![]() .
.


 科学实验活动册系列答案
科学实验活动册系列答案科目:高中数学 来源: 题型:
【题目】上世纪末河南出土的以鹤的尺骨(翅骨)制成的“骨笛”(图1),充分展示了我国古代高超的音律艺术及先进的数学水平,也印证了我国古代音律与历法的密切联系.图2为骨笛测量“春(秋)分”,“夏(冬)至”的示意图,图3是某骨笛的部分测量数据(骨笛的弯曲忽略不计),夏至(或冬至)日光(当日正午太阳光线)与春秋分日光(当日正午太阳光线)的夹角等于黄赤交角.


由历法理论知,黄赤交角近1万年持续减小,其正切值及对应的年代如下表:
黄赤交角 |
|
|
|
|
|
正切值 | 0.439 | 0.444 | 0.450 | 0.455 | 0.461 |
年代 | 公元元年 | 公元前2000年 | 公元前4000年 | 公元前6000年 | 公元前8000年 |
根据以上信息,通过计算黄赤交角,可估计该骨笛的大致年代是( )
A.公元前2000年到公元元年B.公元前4000年到公元前2000年
C.公元前6000年到公元前4000年D.早于公元前6000年
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为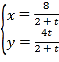 (
(![]() 为参数).以坐标原点
为参数).以坐标原点![]() 为极点,
为极点,![]() 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求直线![]() 的普通方程和曲线
的普通方程和曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)若射线![]() (
(![]() )与直线
)与直线![]() 和曲线
和曲线![]() 分别交于
分别交于![]() ,
,![]() 两点,求
两点,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,过点![]() 的直线l与抛物线
的直线l与抛物线![]() 交于A,B两点,以AB为直径作圆,记为
交于A,B两点,以AB为直径作圆,记为![]() ,
,![]() 与抛物线C的准线始终相切.
与抛物线C的准线始终相切.
(1)求抛物线C的方程;
(2)过圆心M作x轴垂线与抛物线相交于点N,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() 的焦点到直线
的焦点到直线![]() 的距离为
的距离为![]() ,过点
,过点![]() 的直线
的直线![]() 与
与![]() 交于
交于![]() 、
、![]() 两点.
两点.
(1)求抛物线![]() 的准线方程;
的准线方程;
(2)设直线![]() 的斜率为
的斜率为![]() ,直线
,直线![]() 的斜率为
的斜率为![]() ,若
,若![]() ,且
,且![]() 与
与![]() 的交点在抛物线
的交点在抛物线![]() 上,求直线
上,求直线![]() 的斜率和点
的斜率和点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】△ABC中,三个内角A,B,C所对的边分别为a,b,c.且
![]() .
.
(1)若![]() ,求角C的大小.
,求角C的大小.
(2)若AC边上的中线BM的长为2,求△ABC面积的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com