
【题目】已知椭圆C:![]() (a>b>0)的左.右顶点分别为A,B,离心率为
(a>b>0)的左.右顶点分别为A,B,离心率为![]() ,点P
,点P![]() 为椭圆上一点.
为椭圆上一点.
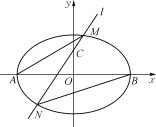
(1) 求椭圆C的标准方程;
(2) 如图,过点C(0,1)且斜率大于1的直线l与椭圆交于M,N两点,记直线AM的斜率为k1,直线BN的斜率为k2,若k1=2k2,求直线l斜率的值.
【答案】(1)![]() +
+![]() =1;(2) k=
=1;(2) k=![]()
【解析】
(1)根据已知条件,建立方程组,求出a,b,即可得到椭圆的标准方程.
(2)设出直线l方程为y=kx+1,M(x1,y1),N(x2,y2),将直线l方程与椭圆方程联立,求出x1+x2和x1x2,根据条件求出k1和k2,代入k1=2k2化简计算,得到关于k的方程,解方程求出k的值.
(1)因为椭圆的离心率为![]() ,所以a=2c.
,所以a=2c.
又因为a2=b2+c2,所以b=![]() c.
c.
所以椭圆的标准方程为![]() +
+![]() =1.
=1.
又因为点P![]() 为椭圆上一点,所以
为椭圆上一点,所以![]() +
+![]() =1,解得c=1.
=1,解得c=1.
所以椭圆的标准方程为![]() +
+![]() =1.
=1.
(2)由椭圆的对称性可知直线l的斜率一定存在,设其方程为y=kx+1.
设M(x1,y1),N(x2,y2).
联立直线![]() 与椭圆的方程组
与椭圆的方程组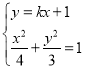 ,消去y可得(3+4k2)x2+8kx-8=0.
,消去y可得(3+4k2)x2+8kx-8=0.
所以由根与系数关系可知x1+x2=-![]() ,x1x2=-
,x1x2=-![]() .
.
因为k1=![]() ,k2=
,k2=![]() ,且k1=2k2,所以
,且k1=2k2,所以![]() =
=![]() .
.
即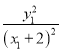 =
=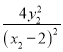 ,①
,①
又因为M(x1,y1),N(x2,y2)在椭圆上,
所以![]() .②
.②
将②代入①可得:![]() =
=![]() ,即3x1x2+10(x1+x2)+12=0.
,即3x1x2+10(x1+x2)+12=0.
所以3![]() +10
+10![]() +12=0,即12k2-20k+3=0.
+12=0,即12k2-20k+3=0.
解得k=![]() 或k=
或k=![]() ,又因为k>1,所以k=
,又因为k>1,所以k=![]() .
.


 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案 蓝天教育暑假优化学习系列答案
蓝天教育暑假优化学习系列答案科目:高中数学 来源: 题型:
【题目】某市为调研学校师生的环境保护意识,决定在本市所有学校中随机抽取60所进行环境综合考评成绩达到80分以上(含80分)为达标.60所学校的考评结果频率分布直方图如图所示(其分组区间为[50,60),[60,70),[70,80),[80,90),[90,100]).

(Ⅰ)试根据样本估汁全市学校环境综合考评的达标率;
(Ⅱ)若考评成绩在[90.100]内为优秀.且甲乙两所学校考评结果均为优秀从考评结果为优秀的学校中随机地抽取两所学校作经验交流报告,求甲乙两所学校至少有一所被选中的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,圆![]() ,
,![]() 是圆M内一个定点,P是圆上任意一点,线段PN的垂直平分线l和半径MP相交于点Q,当点P在圆M上运动时,点Q的轨迹为曲线E.
是圆M内一个定点,P是圆上任意一点,线段PN的垂直平分线l和半径MP相交于点Q,当点P在圆M上运动时,点Q的轨迹为曲线E.
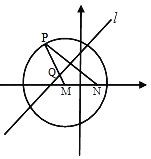
(1)求曲线E的方程;
(2)已知抛物线![]() 上,是否存在直线m与曲线E交于G,H,使得G,H中点F落在直线y=2x上,并且与抛物线相切,若直线m存在,求出直线m的方程,若不存在,说明理由.
上,是否存在直线m与曲线E交于G,H,使得G,H中点F落在直线y=2x上,并且与抛物线相切,若直线m存在,求出直线m的方程,若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若函数![]() 在其图象上存在不同的两点
在其图象上存在不同的两点![]() ,
,![]() ,其坐标满足条件:
,其坐标满足条件: ![]() 的最大值为0,则称
的最大值为0,则称![]() 为“柯西函数”,则下列函数:①
为“柯西函数”,则下列函数:①![]()
![]() :②
:②![]() :③
:③![]() :④
:④![]() .
.
其中为“柯西函数”的个数为( )
A. 1B. 2C. 3D. 4
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com