从1,2,3,4,5中任取2个不同数作和,如果和为偶数得2分,和为奇数得1分,若ξ表示取出后的得分,则Eξ=________.

分析:由题意从1,2,3,4,5中任取2个不同数作和,如果和为偶数得2分,和为奇数得1分,而设ξ表示取出后的得分,由题意ξ的值可以取1,2,利用古典概型的概率公式得到随即变量每一个可能取值下的概率值,在代入期望的定义式即可.
解答:由题意从1,2,3,4,5中任取2个不同数的所有结果为:(1,2),(1,3),(1,4),(1,5),(2,3),(2,4),(2,5),(3,4),(3,5),(4,5)共10种结果,取出的两个数的和为:3,4,5,6,7,8,9,和为3的1中取法,和为4的1中取法,和为5的有(1,4),(2,3)两种取法,和为6的(1,5),(2,4)两种取法,和为7的(2,5),(3,4)两种取法,和为8的(3,5)1中取法,和为9的(4,5)1中取法,利用古典概型事件的概率公式可以得到:
P(ξ=1)=
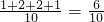
,P(ξ=2)=
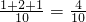
,利用期望公式得:

.
故答案为:

.
点评:此题考查了学生对于题意的理解能力及计算能力,还考查了离散型随机变量的定义及其分布列,离散型随即变量的期望公式.


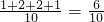 ,P(ξ=2)=
,P(ξ=2)=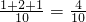 ,利用期望公式得:
,利用期望公式得: .
. .
.

 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案