
【题目】已知椭圆![]() :
:![]() 的离心率为
的离心率为![]() ,以
,以![]() 的四个顶点为顶点的四边形的面积为
的四个顶点为顶点的四边形的面积为![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)设![]() ,
,![]() 分别为椭圆
分别为椭圆![]() 的左、右顶点,
的左、右顶点,![]() 是直线
是直线![]() 上不同于点
上不同于点![]() 的任意一点,若直线
的任意一点,若直线![]() ,
,![]() 分别与椭圆相交于异于
分别与椭圆相交于异于![]() ,
,![]() 的点
的点![]() 、
、![]() ,试探究,点
,试探究,点![]() 是否在以
是否在以![]() 为直径的圆内?证明你的结论.
为直径的圆内?证明你的结论.
 提分百分百检测卷系列答案
提分百分百检测卷系列答案科目:高中数学 来源: 题型:
【题目】某班主任对全班50名学生学习积极性和参加社团活动情况进行调查,统计数据如表所示
参加社团活动 | 不参加社团活动 | 合计 | |
学习积极性高 | 17 | 8 | 25 |
学习积极性一般 | 5 | 20 | 25 |
合计 | 22 | 28 | 50 |
(Ⅰ)如果随机从该班抽查一名学生,抽到参加社团活动的学生的概率是多少?抽到不参加社团活动且学习积极性一般的学生的概率是多少?
(Ⅱ)试运用独立性检验的思想方法分析:学生的学习积极性与参加社团活动情况是否有关系?并说明理由.
x2=![]() .
.
P(x2≥k) | 0.05 | 0.01 | 0.001 |
K | 3.841 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知AB是圆O的直径,C、D是圆O上的两个点,CE⊥AB于E,BD交AC于G,交CE于F,CF=FG.
(Ⅰ)求证:C是劣弧![]() 的中点;
的中点;
(Ⅱ)求证:BF=FG.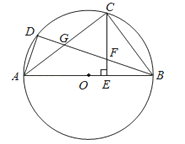
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,角A,B,C的对边分别为a,b,c,且满足bcosA=(2c+a)cos(π﹣B)
(1)求角B的大小;
(2)若b=4,△ABC的面积为![]() , 求a+c的值.
, 求a+c的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列命题中正确的是( )
A.命题p:“?x0∈R, ![]() ”,则命题?p:?x∈R,x2﹣2x+1>0
”,则命题?p:?x∈R,x2﹣2x+1>0
B.“lna>lnb”是“2a>2b”的充要条件
C.命题“若x2=2,则 ![]() 或
或 ![]() ”的逆否命题是“若
”的逆否命题是“若 ![]() 或
或 ![]() ,则x2≠2”
,则x2≠2”
D.命题p:?x0∈R,1﹣x0<lnx0;命题q:对?x∈R,总有2x>0;则p∧q是真命题
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】记min{x,y}= ![]() 设f(x)=min{x2 , x3},则( )
设f(x)=min{x2 , x3},则( )
A.存在t>0,|f(t)+f(﹣t)|>f(t)﹣f(﹣t)
B.存在t>0,|f(t)﹣f(﹣t)|>f(t)﹣f(﹣t)
C.存在t>0,|f(1+t)+f(1﹣t)|>f(1+t)+f(1﹣t)
D.存在t>0,|f(1+t)﹣f(1﹣t)|>f(1+t)﹣f(1﹣t)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com