
【题目】为了检测某种零件的一条生产线的生产过程,从生产线上随机抽取一批零件,根据其尺寸的数据分成![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
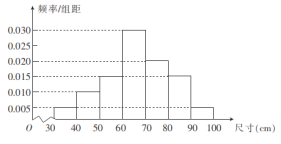
,![]() 组,得到如图所示的频率分布直方图.若尺寸落在区间
组,得到如图所示的频率分布直方图.若尺寸落在区间![]() 之外,则认为该零件属“不合格”的零件,其中
之外,则认为该零件属“不合格”的零件,其中![]() ,
,![]() 分别为样本平均和样本标准差,计算可得
分别为样本平均和样本标准差,计算可得![]() (同一组中的数据用该组区间的中点值作代表).
(同一组中的数据用该组区间的中点值作代表).
(1)若一个零件的尺寸是![]() ,试判断该零件是否属于“不合格”的零件;
,试判断该零件是否属于“不合格”的零件;
(2)工厂利用分层抽样的方法从样本的前![]() 组中抽出
组中抽出![]() 个零件,标上记号,并从这
个零件,标上记号,并从这![]() 个零件中再抽取
个零件中再抽取![]() 个,求再次抽取的
个,求再次抽取的![]() 个零件中恰有
个零件中恰有![]() 个尺寸小于
个尺寸小于![]() 的概率.
的概率.
【答案】(1)该零件属于“不合格”的零件;(2)![]() .
.
【解析】
(1)先由频率分布直方图中的数据,求出样本平均值,得到![]() ,根据题意,即可得出结果;
,根据题意,即可得出结果;
(2)根据分层抽样的方法得到第一组抽![]() 个,记为
个,记为![]() ;第二组抽
;第二组抽![]() 个,记为
个,记为![]() ,
,![]() ;第三组抽
;第三组抽![]() 个,记为
个,记为![]() ,
,![]() ,
,![]() ,用列举法列举出总的基本事件,以及满足条件的基本事件,进而可得出结果.
,用列举法列举出总的基本事件,以及满足条件的基本事件,进而可得出结果.
(1)由频率分布直方图可得,该批零件的样本平均值为:
![]()
![]() ;
;
则![]() ,
,![]() ,
,![]() ,
,
所以该零件属于“不合格”的零件;
(2)按照分层抽样抽![]() 个零件时,第一组抽
个零件时,第一组抽![]() 个,记为
个,记为![]() ;第二组抽
;第二组抽![]() 个,记为
个,记为![]() ,
,![]() ;第三组抽
;第三组抽![]() 个,记为
个,记为![]() ,
,![]() ,
,![]() ,
,
从这![]() 个零件中抽取
个零件中抽取![]() 个零件共有
个零件共有![]() 种情况,分别为
种情况,分别为![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
其中再抽取的![]() 个零件中恰有
个零件中恰有![]() 个尺寸小于
个尺寸小于![]() 的有
的有![]() 种,分别为
种,分别为![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
根据古典概型概率公式,可得![]() .
.


 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案 蓝天教育暑假优化学习系列答案
蓝天教育暑假优化学习系列答案科目:高中数学 来源: 题型:
【题目】对于由有限个自然数组成的集合A,定义集合S(A)={a+b|a∈A,b∈A},记集合S(A)的元素个数为d(S(A)).定义变换T,变换T将集合A变换为集合T(A)=A∪S(A).
(1)若A={0,1,2},求S(A),T(A);
(2)若集合A有n个元素,证明:“d(S(A))=2n-1”的充要条件是“集合A中的所有元素能组成公差不为0的等差数列”;
(3)若A{1,2,3,4,5,6,7,8}且{1,2,3,…,25,26}T(T(A)),求元素个数最少的集合A.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的中心在坐标原点,且经过点
的中心在坐标原点,且经过点![]() ,它的一个焦点与抛物线E:
,它的一个焦点与抛物线E:![]() 的焦点重合,斜率为k的直线l交抛物线E于A、B两点,交椭圆
的焦点重合,斜率为k的直线l交抛物线E于A、B两点,交椭圆![]() 于C、D两点.
于C、D两点.
(1)求椭圆![]() 的方程;
的方程;
(2)直线l经过点![]() ,设点
,设点![]() ,且
,且![]() 的面积为
的面积为![]() ,求k的值;
,求k的值;
(3)若直线l过点![]() ,设直线
,设直线![]() ,
,![]() 的斜率分别为
的斜率分别为![]() ,
,![]() ,且
,且![]() ,
,![]() ,
,![]() 成等差数列,求直线l的方程.
成等差数列,求直线l的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校为了普及环保知识,增强学生的环保意识,在全校组织了一次有关环保知识的竞赛,经过初赛、复赛,甲、乙两个代表队(每队![]() 人)进入了决赛,规定每人回答一个问题,答对为本队赢得
人)进入了决赛,规定每人回答一个问题,答对为本队赢得![]() 分,答错得
分,答错得![]() 分,假设甲队中每人答对的概率均为
分,假设甲队中每人答对的概率均为![]() ,乙队中
,乙队中![]() 人答对的概率分別为
人答对的概率分別为![]() ,且各人回答正确与否相互之间没有影响,用
,且各人回答正确与否相互之间没有影响,用![]() 表示乙队的总得分.
表示乙队的总得分.
(1)求![]() 的分布列;
的分布列;
(2)求甲、乙两队总得分之和等于![]() 分且甲队获胜的概率.
分且甲队获胜的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() ,其左右顶点分别为
,其左右顶点分别为![]() ,
,![]() ,上下顶点分别为
,上下顶点分别为![]() ,
,![]() .圆
.圆![]() 是以线段
是以线段![]() 为直径的圆.
为直径的圆.
(1)求圆![]() 的方程;
的方程;
(2)若点![]() ,
,![]() 是椭圆上关于
是椭圆上关于![]() 轴对称的两个不同的点,直线
轴对称的两个不同的点,直线![]() ,
,![]() 分别交
分别交![]() 轴于点
轴于点![]()
![]() ,求证:
,求证:![]() 为定值;
为定值;
(3)若点![]() 是椭圆Γ上不同于点
是椭圆Γ上不同于点![]() 的点,直线
的点,直线![]() 与圆
与圆![]() 的另一个交点为
的另一个交点为![]() .是否存在点
.是否存在点![]() ,使得
,使得![]() ?若存在,求出点
?若存在,求出点![]() 的坐标,若不存在,说明理由.
的坐标,若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列四个命题中,真命题是( )
A.和两条异面直线都相交的两条直线是异面直线
B.和两条异面直线都相交于不同点的两条直线是异面直线
C.和两条异面直线都垂直的直线是异面直线的公垂线
D.若![]() 、
、![]() 是异面直线,
是异面直线,![]() 、
、![]() 是异面直线,则
是异面直线,则![]() 、
、![]() 是异面直线
是异面直线
查看答案和解析>>
科目:高中数学 来源: 题型:
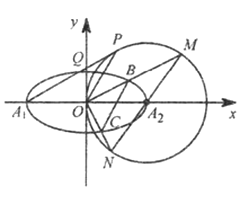
【题目】如图,在平面直角坐标系![]() 中,已知椭圆
中,已知椭圆![]() 的离心率
的离心率![]() ,
,![]() 分别是椭圆
分别是椭圆![]() 的左右两个顶点,圆
的左右两个顶点,圆![]() 的半径为
的半径为![]() ,过点
,过点![]() 作圆
作圆![]() 的切线,切点为
的切线,切点为![]() ,在
,在![]() 轴的上方交椭圆
轴的上方交椭圆![]() 于点
于点![]() .
.
(1)求直线![]() 的方程;
的方程;
(2)求![]() 的值;
的值;
(3)设![]() 为常数,过点
为常数,过点![]() 作两条互相垂直的直线,分别交椭圆于点
作两条互相垂直的直线,分别交椭圆于点![]() ,分别交圆
,分别交圆![]() 于点
于点![]() ,记三角形
,记三角形![]() 和三角
和三角![]() 的面积分别为
的面积分别为![]() .求
.求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 其中a为常数,设e为自然对数的底数.
其中a为常数,设e为自然对数的底数.
(1)当![]() 时,求
时,求![]() 过切点为
过切点为![]() 的切线方程;
的切线方程;
(2)若![]() 在区间
在区间![]() 上的最大值为
上的最大值为![]() ,求a的值;
,求a的值;
(3)若不等式![]() 恒成立,求a的取值范围.
恒成立,求a的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com